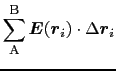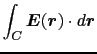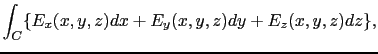: ストークスの定理
: 静電場
: 微分形のガウスの法則
前節では,ナブラ,グラディエント,ダイバージェンスの演算子を扱ったが,今度はローテーションと呼ばれる演算子が登場する.これで電磁気学を学ぶために必要な演算子が揃うことになる.ゴールまであと少しなので,頑張れ!
図1.13に示すように,正電荷 のまわりの空間には静電場
のまわりの空間には静電場 (
( )ができる.この電場の中で,正電荷
)ができる.この電場の中で,正電荷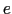 をもつ点電荷を,点A(
をもつ点電荷を,点A(
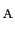 )から,曲線
)から,曲線 に沿って点B(
に沿って点B(
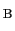 )まで移動させようとすると,
)まで移動させようとすると, (
( )から受ける力
)から受ける力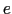
 (
( )に対して外から仕事
)に対して外から仕事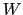 をしなければならない.
をしなければならない.
曲線 上の微小ベクトルを
上の微小ベクトルを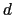
 と書くと,点電荷を
と書くと,点電荷を
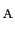 から
から
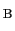 まで移動させるのに必要な仕事の量
まで移動させるのに必要な仕事の量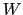 は,
は,
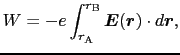 |
|
|
(1.4.56) |
となる.
ここで空間内に任意の曲線 を考え,この曲線上の電場の曲線
を考え,この曲線上の電場の曲線 曲線に沿う方向の成分の和を考えよう.
曲線に沿う方向の成分の和を考えよう.
図1.14のように曲線 を微小線分に分割し,その曲線上の
を微小線分に分割し,その曲線上の
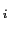 における微小ベクトルを
における微小ベクトルを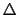

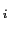 とし,その点における電場を
とし,その点における電場を (
(
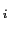 )とおく.そして,
)とおく.そして,
において,曲線の分割を無限に小さくし,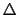
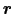
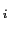
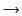 0の極限をとったものを,
0の極限をとったものを,
と書く.これを曲線 に沿う線積分という.
に沿う線積分という.
であるから,上式を成分で表せば,
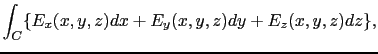 |
|
|
(1.4.57) |
となる.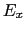 (
( ,
,  ,
,  ),
),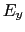 (
( ,
,  ,
,  ),
),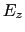 (
( ,
,  ,
,  )は曲線
)は曲線 上の電場である.
上の電場である.
次節では,この線積分の値と道筋の関係を明らかにするために,ストークスの定理について説明しよう.



: ストークスの定理
: 静電場
: 微分形のガウスの法則
Masashige Onoda
平成18年4月15日
![\includegraphics[scale=1, clip]{fig-1-4-1.eps}](img238.png)
![]() のまわりの空間には静電場
のまわりの空間には静電場![]() (
(![]() )ができる.この電場の中で,正電荷
)ができる.この電場の中で,正電荷![]() をもつ点電荷を,点A(
をもつ点電荷を,点A(![]()
![]() )から,曲線
)から,曲線![]() に沿って点B(
に沿って点B(![]()
![]() )まで移動させようとすると,
)まで移動させようとすると,![]() (
(![]() )から受ける力
)から受ける力![]()
![]() (
(![]() )に対して外から仕事
)に対して外から仕事![]() をしなければならない.
をしなければならない.
![]() 上の微小ベクトルを
上の微小ベクトルを![]()
![]() と書くと,点電荷を
と書くと,点電荷を![]()
![]() から
から![]()
![]() まで移動させるのに必要な仕事の量
まで移動させるのに必要な仕事の量![]() は,
は,
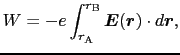
![]() を考え,この曲線上の電場の曲線
を考え,この曲線上の電場の曲線![]() 曲線に沿う方向の成分の和を考えよう.
曲線に沿う方向の成分の和を考えよう.