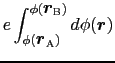: 第3回演習問題
: 静電ポテンシャル
: ベクトル積と回転
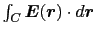 が途中の道筋に依存するかどうかを調べるためには,
が途中の道筋に依存するかどうかを調べるためには, が(1.4.6)式の条件を満たしているかどうかを見ればよい.rot
が(1.4.6)式の条件を満たしているかどうかを見ればよい.rot  (
( )の
)の 成分を計算してみると,
成分を計算してみると,
となる. ,
, 成分に関しても同様に0となるので,
成分に関しても同様に0となるので,
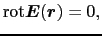 |
|
|
(1.4.67) |
が得られる.
上式を満たしている静電場 (
( )は,一般にある関数
)は,一般にある関数 (
( )の勾配で表すことができる.すなわち,
)の勾配で表すことができる.すなわち,
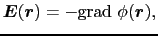 |
|
|
(1.4.68) |
とおける.なぜならば,
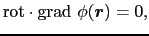 |
|
|
(1.4.69) |
が成立するからである.たとえばrot  grad
grad  (
( )の
)の 成分を計算してみると,
成分を計算してみると,
となる.この (
( )を静電ポテンシャルまたは静電位という.(1.4.13)式の右辺の負の符号は,grad
)を静電ポテンシャルまたは静電位という.(1.4.13)式の右辺の負の符号は,grad  (
( )が
)が (
( )の値の増加方向を向くとした場合,
)の値の増加方向を向くとした場合, (
( )は
)は (
( )の減少方向を向くことによる.
)の減少方向を向くことによる.
静電場 (
( )が(1.1.11)式で与えられているときの,静電ポテンシャル
)が(1.1.11)式で与えられているときの,静電ポテンシャル (
( )の具体的表現は,
)の具体的表現は,
となる.ここで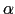 は,
は, ,
, ,
, を意味し,それらの変数で微分をとることを示す.(1.4.13)式と(1.4.15)式とを比較すれば,不定の定数を除いて,
を意味し,それらの変数で微分をとることを示す.(1.4.13)式と(1.4.15)式とを比較すれば,不定の定数を除いて,
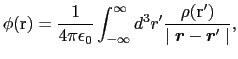 |
|
|
(1.4.71) |
となる.これを(1.4.1)式に代入すると,点電荷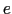 を点
を点
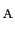 から点
から点
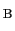 まで移動させるために外部からなす仕事の量
まで移動させるために外部からなす仕事の量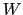 は,
は,
となる.
1 [C]の点電荷を運ぶのに1 [J]の仕事を要するとき,その二点間の電位差を1 [V]という.
1 [V] = 1 [J/C] = 1 [NmA
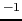
s
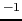
]
1 [NA
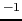
s
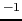
] = 1 [V/m]



: 第3回演習問題
: 静電ポテンシャル
: ベクトル積と回転
Masashige Onoda
平成18年4月15日
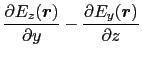
![$\displaystyle {1\over{4\pi\epsilon_0}} \int_{-\infty}^{\infty}d^{3}r'
\rho(\mbo...
... z}}{1\over{\mid \mbox{\boldmath$r$} - \mbox{\boldmath$r$}' \mid^{3}}} \right ]$](img288.png)
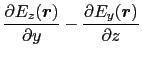
![$\displaystyle {1\over{4\pi\epsilon_0}} \int_{-\infty}^{\infty}d^{3}r'
\rho(\mbo...
... z}}{1\over{\mid \mbox{\boldmath$r$} - \mbox{\boldmath$r$}' \mid^{3}}} \right ]$](img288.png)
![]() (
(![]() )は,一般にある関数
)は,一般にある関数![]() (
(![]() )の勾配で表すことができる.すなわち,
)の勾配で表すことができる.すなわち,
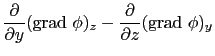
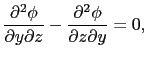
![]() (
(![]() )が(1.1.11)式で与えられているときの,静電ポテンシャル
)が(1.1.11)式で与えられているときの,静電ポテンシャル![]() (
(![]() )の具体的表現は,
)の具体的表現は,
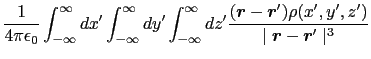
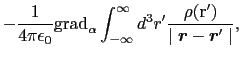
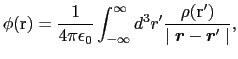
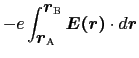
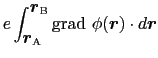
![$\displaystyle e \int_{\mbox{\boldmath$r$}_{\rm A}}^{\mbox{\boldmath$r$}_{\rm B}...
...artial y}}dy +
{\partial \phi(\mbox{\boldmath$r$})\over{\partial z}}dz \right ]$](img303.png)