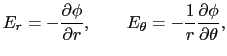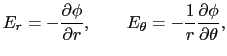: 静電場の基本法則とその応用例
: 静電ポテンシャル
: 静電ポテンシャル
- 無限に長い一様な直線状の電荷の作る静電ポテンシャルを求めよ.ただし,単位長さ当りの電荷量を
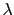 とする(1.1節の例題および第2回演習問題1番を参照のこと).
とする(1.1節の例題および第2回演習問題1番を参照のこと).
- 半径
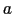 の球内に全電荷
の球内に全電荷 が一様に分布しているときの球内外の静電ポテンシャルを求め図示せよ.ただし球外の静電ポテンシャルは距離無限大で零になるものとする(第2回演習問題3番を参照のこと).
が一様に分布しているときの球内外の静電ポテンシャルを求め図示せよ.ただし球外の静電ポテンシャルは距離無限大で零になるものとする(第2回演習問題3番を参照のこと).
- 一様な面密度
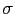 をもち大きさが無限大の電荷平面から距離
をもち大きさが無限大の電荷平面から距離 だけはなれた点の静電ポテンシャルを求めよ(第2回演習問題4番を参照のこと).
だけはなれた点の静電ポテンシャルを求めよ(第2回演習問題4番を参照のこと).
- 2枚の無限に広い平らな板A,Bが,それぞれ面密度
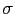 と-
と-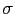 で一様に帯電している.この2枚の板を平行に並べたときの電荷平面A,Bの静電ポテンシャルをそれぞれ
で一様に帯電している.この2枚の板を平行に並べたときの電荷平面A,Bの静電ポテンシャルをそれぞれ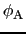 ,
,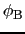 として,電荷面間の静電ポテンシャルの変化を求め図示せよ(第2回演習問題5番を参照のこと).
として,電荷面間の静電ポテンシャルの変化を求め図示せよ(第2回演習問題5番を参照のこと).
 やや難
やや難 二つの正負等量の点電荷+
二つの正負等量の点電荷+ と-
と- がごく短い距離
がごく短い距離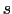 で固定されているものを電気双極子という.-
で固定されているものを電気双極子という.- の電荷から+
の電荷から+ の電荷に向かうベクトルを
の電荷に向かうベクトルを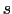 とおいたとき,
とおいたとき,
を電気双極子モーメントベクトルと呼ぶ.分子の中にはこの電気双極子をもったものが種々みられる.電気双極子の中点Oから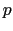 の方向に
の方向に 軸をとり,
軸をとり, 軸から角度
軸から角度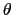 の方向に
の方向に だけはなれた点Pにおける静電場,
だけはなれた点Pにおける静電場,
を求めよ.ただし
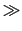
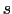 とせよ(この問題は(1.1.7)式で与えられる静電場をベクトル的に重ね合わせることによって解くこともできるが,本節で学んだ静電ポテンシャルを重ね合わせるほうが簡単である).
とせよ(この問題は(1.1.7)式で与えられる静電場をベクトル的に重ね合わせることによって解くこともできるが,本節で学んだ静電ポテンシャルを重ね合わせるほうが簡単である).
Masashige Onoda
平成18年4月15日