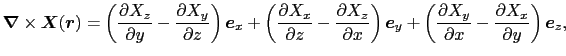: 静電ポテンシャル
: 静電ポテンシャル
: ストークスの定理
ベクトル と
と のベクトル積あるいは外積は,
のベクトル積あるいは外積は,
で表される.その大きさは,これら と
と の作る平行四辺形の面積
の作る平行四辺形の面積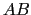 sin
sin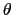 であり,その方向は
であり,その方向は と
と に直交し,
に直交し, から
から に回転したとき,右ねじの進む方向である(図1.18).この種の量は,たとえば物体の角運動量(角運動量 = 腕の長さ
に回転したとき,右ねじの進む方向である(図1.18).この種の量は,たとえば物体の角運動量(角運動量 = 腕の長さ 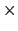 運動量 = 距離
運動量 = 距離 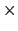 運動量
運動量 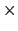 sin
sin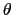 )で現れる.
)で現れる.
この定義から,1.3節で示した直交座標系の基本ベクトルの間には
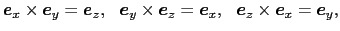 |
|
|
|
| |
|
|
(1.4.62) |
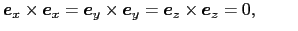 |
|
|
|
の関係がある.また,
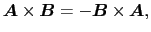 |
|
|
(1.4.63) |
が成り立つ.
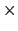
 を
を と
と との成分で表すと,
との成分で表すと,
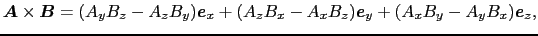 |
|
|
(1.4.64) |
となる.ここで,
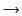
 ,
,
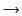
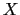 (
( )とおくと,
)とおくと,
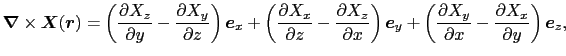 |
|
|
(1.4.65) |
が得られる.こうして,
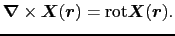 |
|
|
(1.4.66) |



: 静電ポテンシャル
: 静電ポテンシャル
: ストークスの定理
Masashige Onoda
平成18年4月15日
![\includegraphics[scale=0.7, clip]{fig-1-4-6.eps}](img276.png)