


: 第6回演習問題
: 静電場
: 第5回演習問題
これまでは,真空中に電荷があるとき,そのまわりの空間にできる静電場を決定する法則を調べてきた.ファラデーは,コンデンサーの電極板の間に誘電体(不導体)を挿入すると,その静電容量が増大することを発見した.
すべての物質は原子から構成され,原子は正電荷をもつ重い原子核と負電荷をもつ軽い電子からなる.電気的に中性の原子の場合,原子核の正電荷の量と電子の負電荷の量は等しい.ここに外部から電場が作用すると静電誘導により,原子は分極現象を起こす.たとえば,正電荷によって作られた電場が原子に作用すると,クーロン引力により電子は引き寄せられ,原子核は斥けられるために,原子は電気双極子1.4を構成することになる.
帯電体のまわりに誘電体があるとき,誘電体を構成している原子の集団は図1.25のようになっており,多くの電気双極子が分布している.このように分極した多くの原子の間の小さな隙間の電場は,元々の帯電体による電場にその場所のまわりの多くの分極した原子のつくる電場が重ね合わさったもので,その構造は非常に複雑である.ここでは,たくさんの原子を含む領域を対象として,その領域における平均的な電場を考える(原子スケールからみると大きい領域であるが,巨視的な目でみたときには非常に微小な領域である).すなわち,原子は空間内に連続的に分布しているとみなそう.
いま,二枚のシートにそれぞれ正と負の等量の電荷が一様に分布しているとしよう.
外部から電場が作用していないときには,二枚のシートはピタリと重ね合わさっている.次に,外から正電荷による電場が作用すると,負に帯電したシートは少し引き寄せられ,正に帯電したシートは少し斥けられる.重ね合わせたシートを横切る任意の面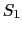 を考えると,正電荷をもつシートが少しずれることによって,この面
を考えると,正電荷をもつシートが少しずれることによって,この面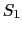 を正電荷が通過することになる.このずらしによって面
を正電荷が通過することになる.このずらしによって面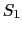 上の単位面積を通過する正電荷の大きさと方向をベクトル
上の単位面積を通過する正電荷の大きさと方向をベクトル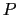 で表す.
で表す.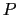 は分極ベクトルと呼ばれる(図1.26).
は分極ベクトルと呼ばれる(図1.26).
このとき正電荷の移動する向きに,面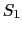 に垂直に立てた単位ベクトルを
に垂直に立てた単位ベクトルを
 とおくと,面
とおくと,面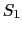 を通過する全正電荷の量は,
を通過する全正電荷の量は,
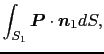 |
|
|
(1.7.99) |
となる.他の面
 に対しても同様に,
に対しても同様に,
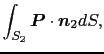 |
|
|
(1.7.100) |
となる.任意の二つの閉曲面
 と
と
 において一般に,
において一般に,
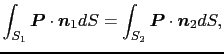 |
|
|
(1.7.101) |
が成立する.
正に帯電している物体Aのまわりに誘電体が分布しているとき,誘電体の存在の効果として現実に我々の目にふれるのは,帯電体Aの表面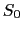 に現れる負電荷だけである.なぜなら,その表面
に現れる負電荷だけである.なぜなら,その表面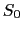 以外の場所では,分極した誘電体の正負の電荷分布は中和しており,また空間を満たす誘電体が無限の広い領域に広がっているとき,しみだした正電荷は無限遠方に現れるからである.この帯電体Aの表面
以外の場所では,分極した誘電体の正負の電荷分布は中和しており,また空間を満たす誘電体が無限の広い領域に広がっているとき,しみだした正電荷は無限遠方に現れるからである.この帯電体Aの表面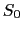 の上に現れる負電荷の値は,
の上に現れる負電荷の値は,
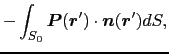 |
|
|
(1.7.102) |
と表される.帯電体を囲む任意の閉曲面 上にガウスの法則を適用すると,
上にガウスの法則を適用すると,
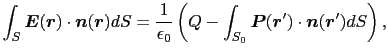 |
|
|
(1.7.103) |
が成立する.ここで は帯電体Aに与えた電荷で,真電荷と呼ばれる.(1.7.3)式から,
は帯電体Aに与えた電荷で,真電荷と呼ばれる.(1.7.3)式から,
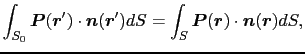 |
|
|
(1.7.104) |
であるから,(1.7.5)式は,
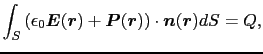 |
|
|
(1.7.105) |
と変形される.これは,真電荷 を真空中においたときのガウスの法則から導かれる電場
を真空中においたときのガウスの法則から導かれる電場
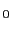 (
( )よりも小さくなっている.すなわち,同じ真電荷
)よりも小さくなっている.すなわち,同じ真電荷 によってつくられる電場の強さが,誘電体のあるときには真空中よりも小さくなる.そのために,同じ強さの電場をつくる真電荷の大きさは,誘電体のあるときのほうが大きくならなければならない.これによりコンデンサーに蓄えられる電荷の量が増大し,その静電容量が大きくなる.
によってつくられる電場の強さが,誘電体のあるときには真空中よりも小さくなる.そのために,同じ強さの電場をつくる真電荷の大きさは,誘電体のあるときのほうが大きくならなければならない.これによりコンデンサーに蓄えられる電荷の量が増大し,その静電容量が大きくなる.
(1.7.7)式の左辺の場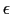
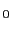
 +
+ 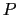 は真電荷だけのつくった場であって,これは
は真電荷だけのつくった場であって,これは
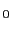 と同じ大きさの値をもつ.いま,
と同じ大きさの値をもつ.いま,
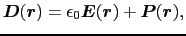 |
|
|
(1.7.106) |
で定義される電束密度を考えよう.これは真空中の
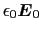 (
( )と同じ役目を果たす.すなわち,
)と同じ役目を果たす.すなわち,
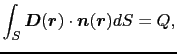 |
|
|
(1.7.107) |
の関係を満たす.
実験によると,多くの誘電体において,
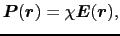 |
|
|
(1.7.108) |
の関係が成り立つ.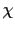 を電気感受率という.この関係式を(1.7.8)式に代入すると,
を電気感受率という.この関係式を(1.7.8)式に代入すると,
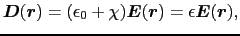 |
|
|
(1.7.109) |
となる.ここで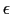 =
= 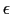
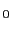 +
+ 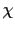 を誘電率という.また,真空の誘電率を単位として測った,
を誘電率という.また,真空の誘電率を単位として測った,
を比誘電率と呼ぶ.
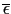 の大きさは,たとえば,ガラスが8.0〜9.0,水(293 [K])が80.36,空気(273 [K],1 [atm])が1.000594,チタン酸バリウム1.5が2000程度である.真空の場合には
の大きさは,たとえば,ガラスが8.0〜9.0,水(293 [K])が80.36,空気(273 [K],1 [atm])が1.000594,チタン酸バリウム1.5が2000程度である.真空の場合には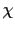 = 0であるので,(1.7.11)式を用いると,ガウスの法則は,真空中,誘電体中を問わず,共通に(1.7.9)式で表すことができる.
= 0であるので,(1.7.11)式を用いると,ガウスの法則は,真空中,誘電体中を問わず,共通に(1.7.9)式で表すことができる.
(1.7.9)式の右辺の真電荷 が連続分布をしているときには,その電荷密度
が連続分布をしているときには,その電荷密度 (
( )を用いて,
)を用いて,
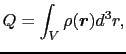 |
|
|
(1.7.110) |
と表される.ここで は(1.7.9)式の閉曲面
は(1.7.9)式の閉曲面 により囲まれる空間的領域である.(1.7.12)式と(1.7.9)式とから,微分形におけるガウスの法則は次のようになる.
により囲まれる空間的領域である.(1.7.12)式と(1.7.9)式とから,微分形におけるガウスの法則は次のようになる.
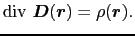 |
|
|
(1.7.111) |
電場 (
( )にとって誘電体の存在は,帯電体の表面上の負の分極電荷の出現のみによって代表されている.これを除けば,電場にとって誘電体の分布している空間は真空と変わらない.すなわち,誘電体のある場合にも,
)にとって誘電体の存在は,帯電体の表面上の負の分極電荷の出現のみによって代表されている.これを除けば,電場にとって誘電体の分布している空間は真空と変わらない.すなわち,誘電体のある場合にも,
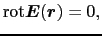 |
|
|
(1.7.112) |
が成立する.



: 第6回演習問題
: 静電場
: 第5回演習問題
Masashige Onoda
平成18年4月15日
![\includegraphics[scale=1, clip]{fig-1-7-1.eps}](img429.png)
![]() に垂直に立てた単位ベクトルを
に垂直に立てた単位ベクトルを![]()
![]() とおくと,面
とおくと,面![]() を通過する全正電荷の量は,
を通過する全正電荷の量は,
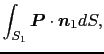
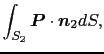
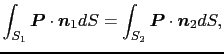
![]() に現れる負電荷だけである.なぜなら,その表面
に現れる負電荷だけである.なぜなら,その表面![]() 以外の場所では,分極した誘電体の正負の電荷分布は中和しており,また空間を満たす誘電体が無限の広い領域に広がっているとき,しみだした正電荷は無限遠方に現れるからである.この帯電体Aの表面
以外の場所では,分極した誘電体の正負の電荷分布は中和しており,また空間を満たす誘電体が無限の広い領域に広がっているとき,しみだした正電荷は無限遠方に現れるからである.この帯電体Aの表面![]() の上に現れる負電荷の値は,
の上に現れる負電荷の値は,
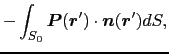
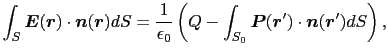
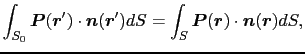
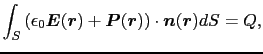
![]()
![]()
![]() +
+ ![]() は真電荷だけのつくった場であって,これは
は真電荷だけのつくった場であって,これは![]()
![]() と同じ大きさの値をもつ.いま,
と同じ大きさの値をもつ.いま,
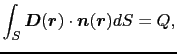
![]() が連続分布をしているときには,その電荷密度
が連続分布をしているときには,その電荷密度![]() (
(![]() )を用いて,
)を用いて,
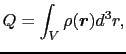
![]() (
(![]() )にとって誘電体の存在は,帯電体の表面上の負の分極電荷の出現のみによって代表されている.これを除けば,電場にとって誘電体の分布している空間は真空と変わらない.すなわち,誘電体のある場合にも,
)にとって誘電体の存在は,帯電体の表面上の負の分極電荷の出現のみによって代表されている.これを除けば,電場にとって誘電体の分布している空間は真空と変わらない.すなわち,誘電体のある場合にも,