


: ホール効果
: 電流と磁場
: 磁気的現象と電気的現象
一つの導線に定常電流を流し,その近くに定常電流を流したもう一つの導線を持ってくると,これらの導線間には力が働く.遠隔作用の立場では,この力は導線間に直接に作用するものと考えるのに対して,近接作用の立場では,一つの導線のまわりの空間に歪みが生じ,その歪んだ状態の空間に他の導線をもってくると,それに力が作用すると解釈する.定常電流によって作られる空間の歪みを「静磁場」という.
実験によると,静磁場の中の定常電流に作用する力の方向は,電流の方向に常に垂直になっている.図3.2にあるように,定常電流の流れている導線を力の作用する方向に垂直な平面内で回転させてみる.導線に作用する力の大きさが最大になったとき,磁場の方向は導線に作用する力の方向と,導線内の定常電流の方向に垂直であると決める.
図 3.2:
静磁場の中の定常電流に作用する力の方向
|
|
導線の長さ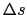 の部分に作用する力の大きさを
の部分に作用する力の大きさを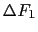 ,定常電流の強さを
,定常電流の強さを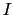 としたとき,静磁場
としたとき,静磁場 の大きさは,
の大きさは,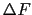 =
= 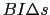 で与えられる.
で与えられる. の大きさは一般に場所
の大きさは一般に場所 の関数である.
の関数である. (
( )を磁束密度と呼ぶ.
)を磁束密度と呼ぶ. (
( )の中に強さ
)の中に強さ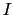 の定常電流をもってくると,これに作用する力
の定常電流をもってくると,これに作用する力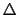
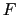 (アンペールの力という)は,
(アンペールの力という)は,
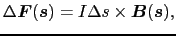 |
|
|
(3.2.1) |
となる.ここで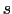 は導線上の点の位置,
は導線上の点の位置,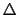
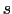 は点
は点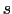 における導線の微小部分である.(3.2.1)式の
における導線の微小部分である.(3.2.1)式の には導線内の定常電流自身の作る静磁場は含まれていない.
には導線内の定常電流自身の作る静磁場は含まれていない.
磁束密度の単位:1 [N A
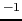
m
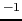
]
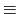
1 [T(テスラ)]
1 [Wb m
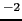
(Wbはウェーバーと呼ぶ)]
(3.2.1)式の力は,導線内の定常電流に作用する力である.電流は電荷の流れであるから,この力を運動する電荷に作用する力として表すことができるはずである.図3.3のような導線上の1点 における微小部分をとり,これに作用するアンペールの力を調べる.導線の単位体積にはたらく力の密度を
における微小部分をとり,これに作用するアンペールの力を調べる.導線の単位体積にはたらく力の密度を (
( )とおくと,
)とおくと,
またその点における電流密度を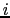 (
( )とすると,
)とすると,
である.したがって,(3.2.1)式は,
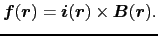 |
|
|
(3.2.2) |
電荷密度を (
( ),その速度を
),その速度を とすると,単位面積の断面を単位時間に通過する電荷量は
とすると,単位面積の断面を単位時間に通過する電荷量は (
( )
) となるので,
となるので,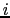 (
( ) =
) =  (
( )
) .したがって(3.2.2)式は,
.したがって(3.2.2)式は,
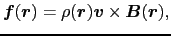 |
|
|
(3.2.3) |
となる.静電場 (
( )と静磁場
)と静磁場 (
( )が共に存在する場合,電荷分布
)が共に存在する場合,電荷分布 (
( )に作用する力の密度は,
)に作用する力の密度は,
![$\displaystyle \mbox{\boldmath$f$}(\mbox{\boldmath$r$})
=
\rho (\mbox{\boldmath$...
... \mbox{\boldmath$v$} \times \mbox{\boldmath$B$}(\mbox{\boldmath$r$}) \right ] ,$](img533.png) |
|
|
(3.2.4) |
領域 内に分布する全電荷に作用する力は,
内に分布する全電荷に作用する力は,
![$\displaystyle \mbox{\boldmath$F$}
=
\int_{V} \mbox{\boldmath$f$}(\mbox{\boldmat...
... \mbox{\boldmath$v$} \times \mbox{\boldmath$B$}(\mbox{\boldmath$r$}) \right ] ,$](img534.png) |
|
|
(3.2.5) |
となる.いま(3.2.5)式の電荷が領域 内の
内の
 の位置に存在する点電荷
の位置に存在する点電荷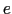 であるときには,
であるときには, (
( ) =
) = 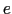
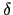
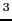 (
( -
- 
 )であるから,
)であるから,
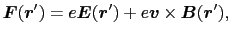 |
|
|
(3.2.6) |
を得る.これをローレンツ力という.



: ホール効果
: 電流と磁場
: 磁気的現象と電気的現象
Masashige Onoda
平成18年4月15日
![\includegraphics[scale=1, clip]{fig-3-2-1.eps}](img522.png)
![]() の部分に作用する力の大きさを
の部分に作用する力の大きさを![]() ,定常電流の強さを
,定常電流の強さを![]() としたとき,静磁場
としたとき,静磁場![]() の大きさは,
の大きさは,![]() =
= ![]() で与えられる.
で与えられる.![]() の大きさは一般に場所
の大きさは一般に場所![]() の関数である.
の関数である.![]() (
(![]() )を磁束密度と呼ぶ.
)を磁束密度と呼ぶ.![]() (
(![]() )の中に強さ
)の中に強さ![]() の定常電流をもってくると,これに作用する力
の定常電流をもってくると,これに作用する力![]()
![]() (アンペールの力という)は,
(アンペールの力という)は,
![]() における微小部分をとり,これに作用するアンペールの力を調べる.導線の単位体積にはたらく力の密度を
における微小部分をとり,これに作用するアンペールの力を調べる.導線の単位体積にはたらく力の密度を![]() (
(![]() )とおくと,
)とおくと,
![$\displaystyle \mbox{\boldmath$F$}
=
\int_{V} \mbox{\boldmath$f$}(\mbox{\boldmat...
... \mbox{\boldmath$v$} \times \mbox{\boldmath$B$}(\mbox{\boldmath$r$}) \right ] ,$](img534.png)