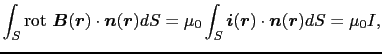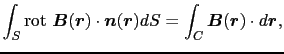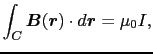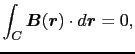

: 第10回演習問題
: 電流と磁場
: 定常電流間に作用する力
ビオとサバールの法則(3.4.3)式は,線状の導線回路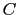 に定常電流
に定常電流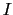 が流れているときに,場所
が流れているときに,場所 につくられる静磁場を与える.導線回路の太さが無視できない場合には,(3.4.3)式を,
につくられる静磁場を与える.導線回路の太さが無視できない場合には,(3.4.3)式を,
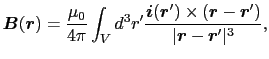 |
|
|
(3.6.15) |
のように一般化する.ここで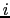 (
( )は電流密度を表し,積分範囲は電流密度の存在する領域全体にわたる.しかしこの積分は複雑で,これを解析的に実行できるのは限られた場合だけである.そこで(3.6.1)式を,
)は電流密度を表し,積分範囲は電流密度の存在する領域全体にわたる.しかしこの積分は複雑で,これを解析的に実行できるのは限られた場合だけである.そこで(3.6.1)式を,
と変形する.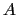 (
( )をベクトルポテンシャルという.
)をベクトルポテンシャルという.
上の証明を行ってみよう.(3.6.2)式,(3.6.3)式から出発して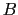
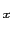 (
( )を計算すると,
)を計算すると,
となり,これは確かに(3.6.1)式の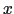 成分に対応する.
成分に対応する.
さてベクトル解析の公式によると,一般に,
が成り立つ.なぜなら,
であるからである.この関係を用いると,(3.6.3)式より,
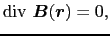 |
|
|
(3.6.18) |
となる.これは磁場に関するガウスの法則で,磁荷密度というものが存在しないことを示している.すなわち,
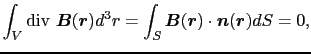 |
|
|
(3.6.19) |
を意味する.これが静磁場における積分形のガウスの法則である.
次に(3.6.2)式の回転を計算してみよう.再びベクトル解析の公式から,
が成り立つ.なぜなら,rot rot 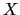 (
( )の
)の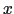 成分は,
成分は,
であるからである.(3.6.2),(3.6.3)式を上の関係に代入すると,
を得る.(3.6.6)式の右辺の第1項には,
の形が出てくる.ここで,この右辺の第1項は,
となるので3.2,
を得る.こうして,
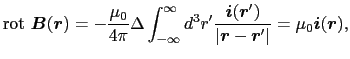 |
|
|
(3.6.21) |
となる.ここで最後の式変形にはポアッソン方程式(1.5.6)式および静電ポテンシャル(1.4.16)式を利用した.(3.6.7)式を微分形のアンペールの法則という.
今,定常電流を囲む閉曲線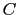 を考え,この閉曲線によって囲まれる任意の曲面
を考え,この閉曲線によって囲まれる任意の曲面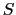 上で(3.6.7)式の面積分を行ってみると,
上で(3.6.7)式の面積分を行ってみると,
となる.ここで曲面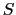 を通過する全電流の強さを
を通過する全電流の強さを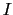 とした.さらに,
とした.さらに,
であるので,
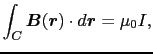 |
|
|
(3.6.22) |
が導かれる.もし閉曲線が電流を囲まないときは,
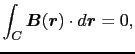 |
|
|
(3.6.23) |
である.(3.6.8)式および(3.6.9)式が積分形のアンペールの法則である.

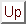

: 第10回演習問題
: 電流と磁場
: 定常電流間に作用する力
Masashige Onoda
平成18年4月15日
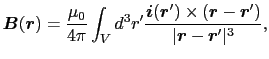
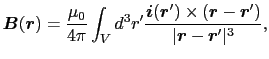
![]()
![]() (
(![]() )を計算すると,
)を計算すると,
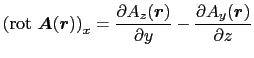
![$\displaystyle {\mu_{0} \over{4 \pi}}
\left [{\partial \over{\partial y}} \int_{...
...ath$r$}') \over{\vert\mbox{\boldmath$r$} - \mbox{\boldmath$r$}'\vert}} \right ]$](img602.png)
![$\displaystyle {\mu_{0} \over{4 \pi}}\int_{V} d^{3}r'
\left [i_{z}(\mbox{\boldma...
...ial z}}{1 \over{\vert\mbox{\boldmath$r$} - \mbox{\boldmath$r$}'\vert}} \right ]$](img603.png)
![$\displaystyle {\mu_{0} \over{4 \pi}}\int_{V} d^{3}r'
\left [-{i_{z}(\mbox{\bold...
...- z') \over{\vert\mbox{\boldmath$r$} - \mbox{\boldmath$r$}'\vert^{3}}} \right ]$](img604.png)
![$\displaystyle {\mu_{0} \over{4 \pi}}\int_{V} d^{3}r'
{\left [\mbox{\boldmath$i$...
... \right ]_{x} \over{\vert\mbox{\boldmath$r$} - \mbox{\boldmath$r$}'\vert^{3}}},$](img605.png)
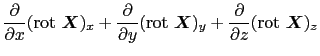
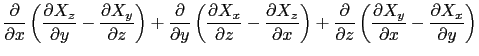
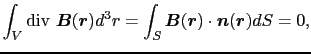
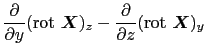
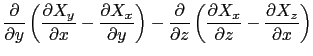
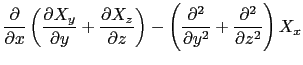
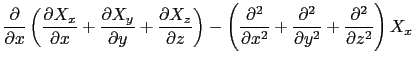
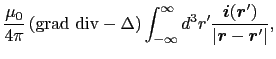
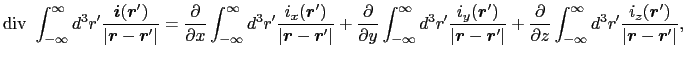
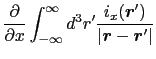
![$\displaystyle \int_{-\infty}^{\infty} d^{3}r' \left [ {\partial \over{\partial ...
...{\boldmath$r$}-\mbox{\boldmath$r$}' \vert}}\right ] i_{x}(\mbox{\boldmath$r$}')$](img624.png)
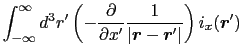
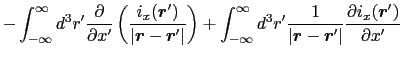
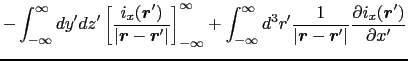
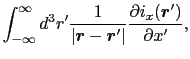
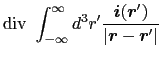
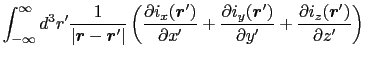
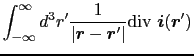
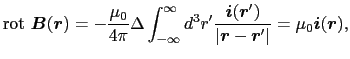
![]() を考え,この閉曲線によって囲まれる任意の曲面
を考え,この閉曲線によって囲まれる任意の曲面![]() 上で(3.6.7)式の面積分を行ってみると,
上で(3.6.7)式の面積分を行ってみると,