: 第14回演習問題
: 波動
: 第13回演習問題
(7.1.4),(7.1.6)式を満たす関数として,様々な波動が挙げられる.図7.4に代表例を示す.
図 7.4:
(7.1.4),(7.1.6)式を満たす波動の例
|
|
これらのうち最も基本的なものが正弦波である.その理由は,数学的表現が簡単であり,また,他の形の波はフーリエ級数とフーリエ積分によってすべて正弦波の重ね合わせで表せるからである.正弦波は,
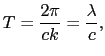 |
|
|
(7.2.14) |
で表される. は振幅,
は振幅,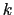 は波数(2
は波数(2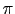 に含まれる波の数)である.
に含まれる波の数)である. に関する周期,
に関する周期,
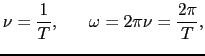 |
|
|
(7.2.15) |
は波長, に関する周期,
に関する周期,
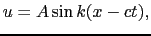 |
|
|
(7.2.16) |
は周期と呼ばれる.また,
 |
|
|
(7.2.17) |
は,それぞれ振動数および角振動数と呼ばれる.
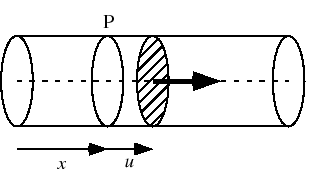
図7.5のように,密度 ,ヤング率
,ヤング率 の一様な弾性体の棒の軸(
の一様な弾性体の棒の軸( 軸)方向に縦波,
軸)方向に縦波,
が進む場合のエネルギーの流れを求めてみよう.波のない状態で の位置にある断面Pを考える.
の位置にある断面Pを考える.
図 7.5:
密度 ,ヤング率
,ヤング率 の一様な弾性体の棒の軸(
の一様な弾性体の棒の軸( 軸)方向に進む縦波
軸)方向に進む縦波
|
|
波は の正方向に伝わりPの位置が移動するので,Pの-側が+側に仕事をする.Pに現れる応力は,
の正方向に伝わりPの位置が移動するので,Pの-側が+側に仕事をする.Pに現れる応力は,
棒の断面積を とすると,このときPの-側が+側におよぼす力は,
とすると,このときPの-側が+側におよぼす力は,
一方,微小時間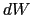 の間にPは(
の間にPは(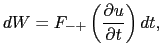
 /
/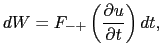
 )
)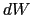 だけ移動するから,その間に力がする仕事を
だけ移動するから,その間に力がする仕事を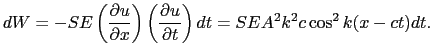 とすると,
とすると,
となる.したがって,
単位断面積,単位時間当りのエネルギーは,
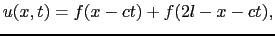 |
|
|
(7.2.18) |
すなわち,波の強さは振幅の2乗と振動数の2乗に比例する.
媒質中を伝わる波が別の媒質に達すると,その境界面で反射されたり,別の媒質中に透過し境界面で屈折が起きたりする. の正の方向に
の正の方向に (
( ,
,  ) =
) =  (
( -
-  )で表される波が,
)で表される波が, =
= 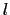 のところで固定端または自由端に達する場合を考えよう.
のところで固定端または自由端に達する場合を考えよう.
- 固定端
 (
( ,
,  )は,
)は, =
= 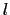 で
で の値によらず必ず0である.そのためには,
の値によらず必ず0である.そのためには,
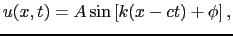 |
|
|
(7.2.19) |
とおけばよい.これは入射波 (
( -
-  )に対し,-
)に対し,-  (2
(2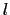 -
-  -
-  )で表される反射波(
)で表される反射波( の負の向きに進む)が新しく加わったと考えることができる.
の負の向きに進む)が新しく加わったと考えることができる.
- 自由端
- 変位でなく応力が0になるので,
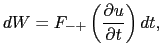
 /
/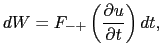
 = 0が条件になる.
= 0が条件になる.
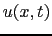 |
|
|
(7.2.20) |
とおけば, =
= 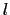 の点では
の点では によらず
によらず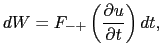
 /
/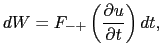
 = 0になる.
= 0になる.
固定端でも自由端でも入射波が反射されることに変わりはない.入射波が,
![$\displaystyle u(x, t)
=
A \sin \left [ k(x - ct) + \phi \right ],$](img939.png) |
|
|
(7.2.21) |
で表される正弦波の場合,同じ振幅で反対向きの正弦波が反射波として生じる.入射波と反射波を重ねると,
上式は, (
( -
-  )とか
)とか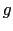 (
( +
+  )のように
)のように 軸に沿って進む波の関数にはなっていない.つまり,ある
軸に沿って進む波の関数にはなっていない.つまり,ある の位置では振幅が定まっており,それぞれの場所では振動数や位相の等しい単振動がその定められた振幅をもって繰り返すだけで,波としては進まない.このような波を定常波という.それに対し進む波のことを進行波という.
の位置では振幅が定まっており,それぞれの場所では振動数や位相の等しい単振動がその定められた振幅をもって繰り返すだけで,波としては進まない.このような波を定常波という.それに対し進む波のことを進行波という.
(7.2.9)式から,
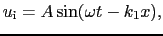 |
|
|
(7.2.23) |
を満たす点 では常に
では常に = 0となる.これらの点を定常波の節という.一方,
= 0となる.これらの点を定常波の節という.一方,
 |
|
|
(7.2.24) |
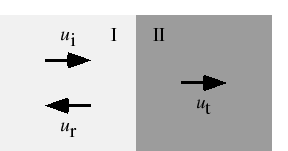
となる点 では振幅が最も大きくなる.これらの点を定常波の腹という.
では振幅が最も大きくなる.これらの点を定常波の腹という.
固定端や自由端では入射波はすべて反射されるが,たとえば,弦の端に線密度の異なる別の弦をつないだとすると,入射波の一部はこの弦にも伝わっていく.すなわち,入射波の一部は透過する.図7.6のように媒質IとIIが接し,媒質Iの中を入射波,
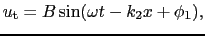 |
|
|
(7.2.25) |
が進むとする.
図 7.6:
媒質IとIIの境界面における入射波,透過波,反射波
|
|
媒質の境界面のところで一部は,透過波,
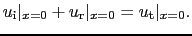 |
|
|
(7.2.26) |
となり媒質IIに入り,一部は,反射波,
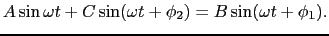 |
|
|
(7.2.27) |
となって媒質Iの中を戻るとする.ここで,媒質が違っても角振動数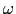 は変化しないが,波の速さが異なるため波長が変化し,波数も変化することに注意しよう.
は変化しないが,波の速さが異なるため波長が変化し,波数も変化することに注意しよう.
境界面では,媒質Iの変位と媒質IIの変位は同じでなければならないことから,
すなわち,
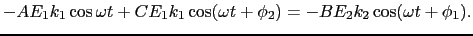 |
|
|
(7.2.28) |
第2の条件として,媒質中の応力も境界面の両側で等しくなければならない.縦波を考え,両媒質のヤング率を
 ,
,
 とすると,
とすると,
すなわち,
ここで,両媒質の密度を
 ,
,
 ,両媒質中での波の速さを
,両媒質中での波の速さを
 ,
,
 とすると,
とすると,
また,
以上より,
したがって,第2の条件は,
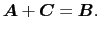 |
|
|
(7.2.29) |
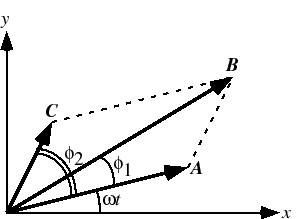
(7.2.15)式の関係は,図7.7のように,角速度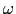 で回転する三つのベクトル
で回転する三つのベクトル ,
, ,
, の
の 軸上への正射影とみることができる.
軸上への正射影とみることができる.
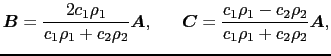 |
|
|
(7.2.30) |
一方,(7.2.16)式から,
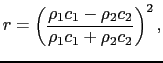 |
|
|
(7.2.31) |
が成立するので,
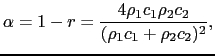 |
|
|
(7.2.32) |
が得られる.これから,
 ,
, ,
, は同じ方向のベクトル.
は同じ方向のベクトル.
 と
と は向きが等しいので,
は向きが等しいので,
 = 0.
= 0.




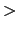



 のとき,
のとき, と
と は向きが同じなので,
は向きが同じなので,
 = 0.
= 0.




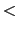



 のとき,
のとき, と
と は向きが逆なので,
は向きが逆なので,
 =
= 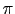 .
.



 =
= 


 のとき,
のとき, = 0なので,反射波はない.
= 0なので,反射波はない.
などが言える.
反射波と入射波の振幅の二乗比,
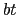 |
|
|
(7.2.33) |
を反射率という.また,透過波と入射波の強さの比,
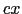 |
|
|
(7.2.34) |
を透過率という.



: 第14回演習問題
: 波動
: 第13回演習問題
Masashige Onoda
平成18年4月15日
![\includegraphics[scale=0.5, clip]{fig-7-2-0.eps}](img922.png)
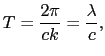
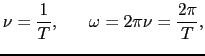

![]() ,ヤング率
,ヤング率![]() の一様な弾性体の棒の軸(
の一様な弾性体の棒の軸(![]() 軸)方向に縦波,
軸)方向に縦波,
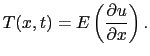
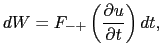
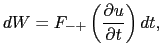
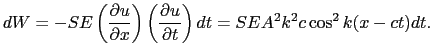 とすると,
とすると,
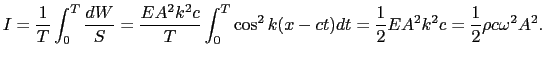
![]() の正の方向に
の正の方向に![]() (
(![]() ,
, ![]() ) =
) = ![]() (
(![]() -
-  )で表される波が,
)で表される波が,![]() =
= ![]() のところで固定端または自由端に達する場合を考えよう.
のところで固定端または自由端に達する場合を考えよう.
 )に対し,-
)に対し,-  )で表される反射波(
)で表される反射波(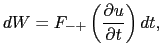
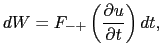
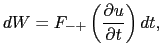
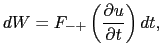
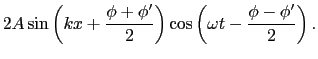
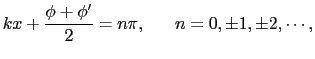
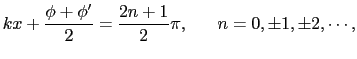
 )とか
)とか )のように
)のように
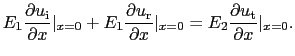
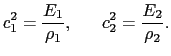
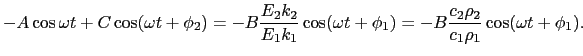
![]() で回転する三つのベクトル
で回転する三つのベクトル![]() ,
,![]() ,
,![]() の
の![]() 軸上への正射影とみることができる.
軸上への正射影とみることができる.