


: 光の干渉
: 波動
: 第14回演習問題
光は波のひとつで,その速さ は真空中を伝わる場合で約3.0
は真空中を伝わる場合で約3.0 10
10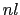 [m/s]である.光が,真空でなく,空気や水などの媒質(屈折率
[m/s]である.光が,真空でなく,空気や水などの媒質(屈折率 )中を伝わるときの速さは,
)中を伝わるときの速さは,
 |
|
|
(7.3.35) |
屈折率 の媒質中の1点Aから距離
の媒質中の1点Aから距離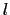 だけ離れた別の点Bまで光が到達するのに要する時間は,
だけ離れた別の点Bまで光が到達するのに要する時間は,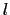 /
/ =
= 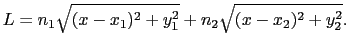 /
/ になる.光の伝搬距離と屈折率との積
になる.光の伝搬距離と屈折率との積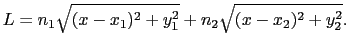 は光学距離と呼ばれる.
は光学距離と呼ばれる.
光が点Aを出て他の点Bへ到達するとき,途中の光線の経路に関しては幾何学的に無数の可能性がある.しかし,空気のような均質な媒質中で観察する限り,光線の経路はAとBを結ぶ直線だけであって,それ以外の経路はない.一般には,媒質が均一でない場合も含め,点Aを出て点Bへ達する光線の経路は,AとBを固定したまま途中を微小変化させてできる他のあらゆる仮想的な経路と比べて,通過に要する時間が極小になるという法則から,光線の経路が決定される.この法則をフェルマーの原理という.
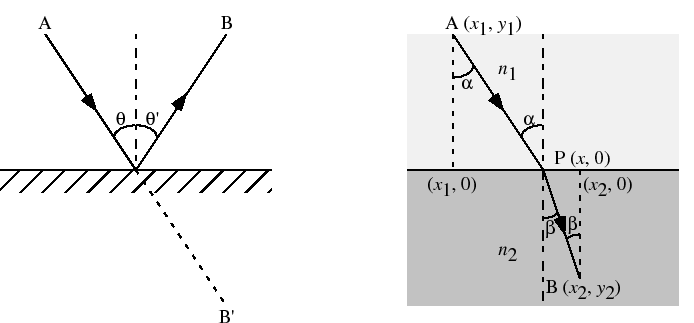
均一な媒質中における光の直進性は,フェルマーの原理から明らかである.入射角と反射角が等しいという反射の法則も,図7.8のように,反射面に関する点Bの鏡像点B を考えれば,明らかである.
を考えれば,明らかである.
図 7.8:
フェルマーの原理に基づく反射と屈折の法則
|
|
フェルマーの原理に基づいて屈折の法則を導いてみよう.屈折率
 の媒質中にある点A(
の媒質中にある点A(
 ,
, 
 )から境界面を経て,屈折率
)から境界面を経て,屈折率
 の媒質中にある点B(
の媒質中にある点B(
 ,
, 
 )へ光が進む場合を考える.境界面においては座標が(
)へ光が進む場合を考える.境界面においては座標が( , 0)で表される点Pを通るとすると,AからBまでの光学距離
, 0)で表される点Pを通るとすると,AからBまでの光学距離 は,
は,
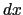 |
|
|
(7.3.36) |
フェルマーの原理により,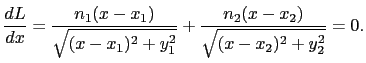 /
/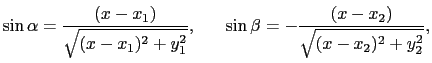 = 0を満たす点Pを光は通過する.すなわち,
= 0を満たす点Pを光は通過する.すなわち,
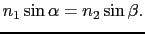 |
|
|
(7.3.37) |
図7.8より,
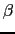 |
|
|
(7.3.38) |
が成り立つので,
 |
|
|
(7.3.39) |
レンズや球面鏡などを用いると,いろいろな像を作ることができる.このような像のでき方とか像の性質などを扱うには,幾何光学という手法が用いられる.幾何光学では,扱う物体が光の波長に比べて十分に大きいため,波の波動性は全く無視し,光線を幾何学的な線として扱う.
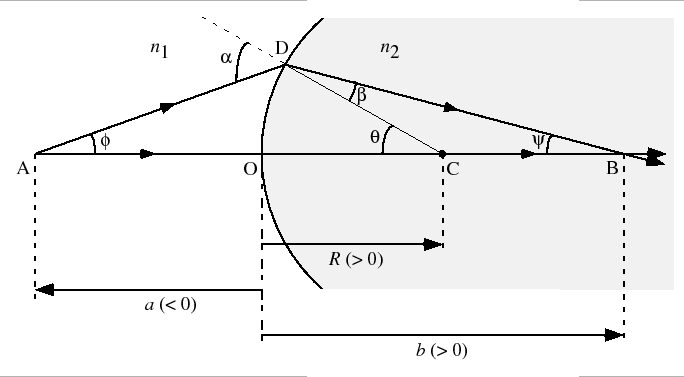
図7.9のように,中心C,半径 の球面を境界にして,屈折率
の球面を境界にして,屈折率
 ,
,
 の媒質が接しているとき,点Aから出た光の屈折について考えよう.すなわち,光が境界面の点Dで屈折し,ACを結ぶ軸と点Bで交わる場合のBの位置を求める.この点での入射角と屈折角は,それぞれ
の媒質が接しているとき,点Aから出た光の屈折について考えよう.すなわち,光が境界面の点Dで屈折し,ACを結ぶ軸と点Bで交わる場合のBの位置を求める.この点での入射角と屈折角は,それぞれ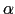 と
と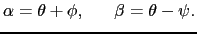 である.
である.
図 7.9:
中心C,半径 の球面を境界にして,屈折率
の球面を境界にして,屈折率
 ,
,
 の媒質が接しているときの,点Aから出た光の屈折
の媒質が接しているときの,点Aから出た光の屈折
|
|
幾何学的関係から,
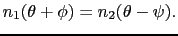 |
|
|
(7.3.40) |
屈折の法則から,
 |
|
|
(7.3.41) |
 ,
,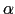 ,
,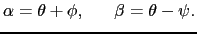 などの角度が小さい場合を考えれば,
などの角度が小さい場合を考えれば,
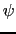 |
|
|
(7.3.42) |
が成り立つので,(7.3.7)式は,
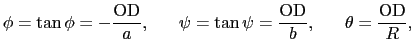 |
|
|
(7.3.43) |
 ,
,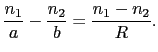 が小さければ,
が小さければ,
 |
|
|
(7.3.44) |
が成り立つので,これらを(7.3.9)式に代入すると,
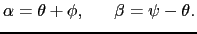 |
|
|
(7.3.45) |
この関係式は,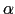 ,
,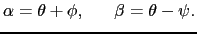 ,
,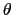 などを含んでいないため,点Aを出た光線はすべて点Bを通ることを意味する.BをAの実像という.
などを含んでいないため,点Aを出た光線はすべて点Bを通ることを意味する.BをAの実像という.
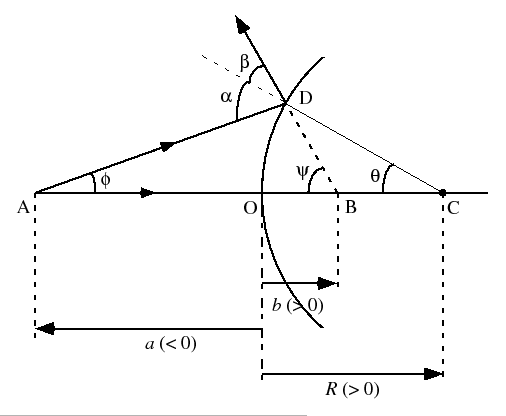
次に,屈折球面の代りに同じ形の球面鏡を考えてみよう.図7.10のように点Aを出た光が球面鏡で反射し,その反射光線の延長戦がAC軸と点Bで交わるものとする.
幾何学的関係から,
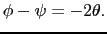 |
|
|
(7.3.46) |
反射の法則から,
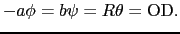 |
|
|
(7.3.47) |
したがって,
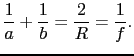 |
|
|
(7.3.48) |
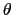 ,
, ,
,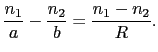 が小さい場合には,
が小さい場合には,
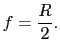 |
|
|
(7.3.49) |
この関係を(7.3.14)式に代入すると,
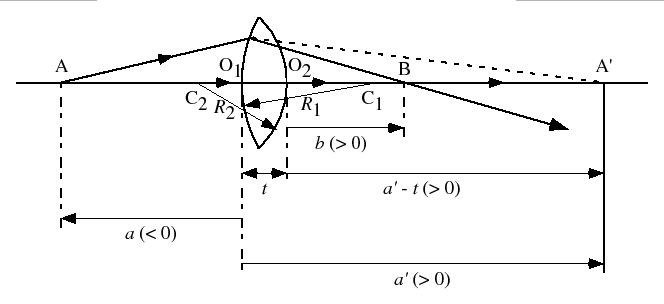 |
|
|
(7.3.50) |
ただし,
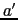 |
|
|
(7.3.51) |
上式で定義される を焦点距離という.光は反射の後,あたかも点Bから出たように進むので,点BをAの虚像という.
を焦点距離という.光は反射の後,あたかも点Bから出たように進むので,点BをAの虚像という.
光がレンズを通るときは,二つの球面で屈折する.両球面の曲率中心を結ぶ直線を光学系の光軸という.図7.11のように,屈折率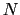 の媒質中に,球面の曲率半径が
の媒質中に,球面の曲率半径が
 と
と
 で屈折率
で屈折率 のレンズがある.
のレンズがある.
図 7.11:
屈折率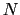 の媒質中における,光軸上の点Aの,球面曲率半径
の媒質中における,光軸上の点Aの,球面曲率半径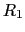 ,
,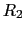 ,屈折率
,屈折率 のレンズによる像B
のレンズによる像B
|
|
二つの球面が光軸を切る点をO ,O
,O とおく.このとき,光軸上の点Aのレンズによる像Bの位置を求めよう.第一の球面によるAの像A
とおく.このとき,光軸上の点Aのレンズによる像Bの位置を求めよう.第一の球面によるAの像A の座標を
の座標を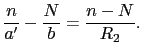 とすると,(7.3.11)式より,
とすると,(7.3.11)式より,
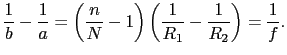 |
|
|
(7.3.52) |
A を新しい光源としたときの第二の球面による像Bが,求めるレンズの像である.ここでは座標の原点がO
を新しい光源としたときの第二の球面による像Bが,求めるレンズの像である.ここでは座標の原点がO となる.
となる.
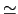 |
|
|
(7.3.53) |
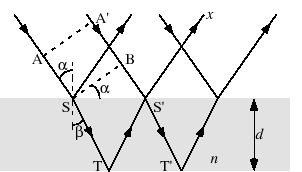
(7.3.18),(7.3.19)式から,
 |
|
|
(7.3.54) |
媒質を空気とすると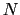
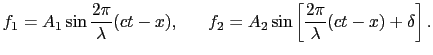 1であるから,
1であるから, /
/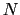 は必ず1より大きい.したがって,両凸レンズ(
は必ず1より大きい.したがって,両凸レンズ(

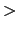 0,
0,

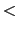 0)では
0)では
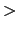 0,両凹レンズ(
0,両凹レンズ(

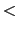 0,
0,

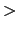 0)では
0)では
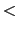 0となる.一般に,中央が周辺より厚い凸レンズでは焦点距離は正,中央が周辺より薄い凹レンズでは焦点距離は負になる.
0となる.一般に,中央が周辺より厚い凸レンズでは焦点距離は正,中央が周辺より薄い凹レンズでは焦点距離は負になる.



: 光の干渉
: 波動
: 第14回演習問題
Masashige Onoda
平成18年4月15日


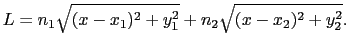 /
/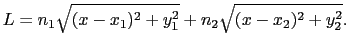 は光学距離と呼ばれる.
は光学距離と呼ばれる.
![]() を考えれば,明らかである.
を考えれば,明らかである.
![]()
![]() の媒質中にある点A(
の媒質中にある点A(![]()
![]() ,
, ![]()
![]() )から境界面を経て,屈折率
)から境界面を経て,屈折率![]()
![]() の媒質中にある点B(
の媒質中にある点B(![]()
![]() ,
, ![]()
![]() )へ光が進む場合を考える.境界面においては座標が(
)へ光が進む場合を考える.境界面においては座標が(![]() , 0)で表される点Pを通るとすると,AからBまでの光学距離
, 0)で表される点Pを通るとすると,AからBまでの光学距離 は,
は,
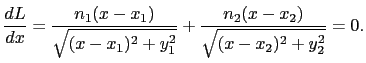 /
/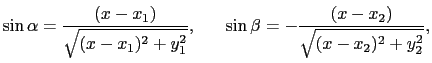 = 0を満たす点Pを光は通過する.すなわち,
= 0を満たす点Pを光は通過する.すなわち,

![]() の球面を境界にして,屈折率
の球面を境界にして,屈折率![]()
![]() ,
,![]()
![]() の媒質が接しているとき,点Aから出た光の屈折について考えよう.すなわち,光が境界面の点Dで屈折し,ACを結ぶ軸と点Bで交わる場合のBの位置を求める.この点での入射角と屈折角は,それぞれ
の媒質が接しているとき,点Aから出た光の屈折について考えよう.すなわち,光が境界面の点Dで屈折し,ACを結ぶ軸と点Bで交わる場合のBの位置を求める.この点での入射角と屈折角は,それぞれ![]() と
と![]() である.
である.

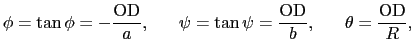
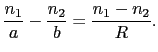 が小さければ,
が小さければ,

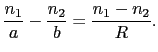 が小さい場合には,
が小さい場合には,
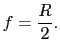

![]() の媒質中に,球面の曲率半径が
の媒質中に,球面の曲率半径が![]()
![]() と
と![]()
![]() で屈折率
で屈折率![]() のレンズがある.
のレンズがある.
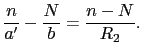 とすると,(7.3.11)式より,
とすると,(7.3.11)式より,
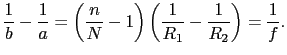

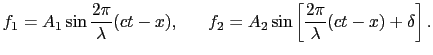 1であるから,
1であるから,