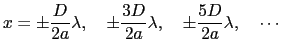: 第15回演習問題
: 波動
: フェルマーの原理と幾何光学
二つ以上の波が同時に1点に到達したとき,波同士が互いに強め合ったり弱め合ったりする現象を,波の干渉という.薄膜を例にして説明しよう.水面に浮かぶ油の薄膜や,シャボン玉が色づいて見えることは,日常的に経験している.
図7.12のように,屈折率 の物質でつくられた厚さ
の物質でつくられた厚さ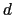 の一様な薄膜に,空気中から波長
の一様な薄膜に,空気中から波長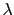 の光が入射角
の光が入射角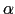 で入射する.
で入射する.
図 7.12:
屈折率 ,厚さ
,厚さ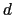 の薄膜に,空気中から波長
の薄膜に,空気中から波長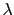 の光が入射角
の光が入射角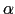 で入射する場合
で入射する場合
|
|
光の一部は表面Sで反射されるが,残りの部分は膜の中に屈折して入り,膜の裏面Tで反射され,S で空気中に出てくる.
で空気中に出てくる.
遠方から薄膜表面の狭い部分に到達する入射光は,平行光線と考えてよいだろう.図のAA やSBでは位相が等しくなっている.一方,A
やSBでは位相が等しくなっている.一方,A からS
からS へきてそこで反射される波と,AからTを経てS
へきてそこで反射される波と,AからTを経てS から空気中へ出ていく波とでは,位相は異なる.
から空気中へ出ていく波とでは,位相は異なる.
二つの波の進行方向に 軸をとり,両者とも正弦波で位相差を
軸をとり,両者とも正弦波で位相差を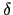 とすると,
とすると,
![$\displaystyle f_{1}
=
A_{1} \sin {2\pi \over{\lambda}}(ct - x), \ \ \ \ \
f_{2}
=
A_{2} \sin \left [ {2\pi \over{\lambda}}(ct - x) + \delta \right ].$](img998.png) |
|
|
(7.4.55) |
重ね合せの原理にしたがって,
 と
と
 を合成すると,
を合成すると,
![$\displaystyle f
=
f_{1} + f_{2}
=
A \sin \left [ {2\pi \over{\lambda}}(ct - x) + \Delta \right ],$](img999.png) |
|
|
(7.4.56) |
ここで,
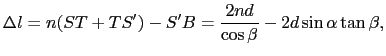 |
|
|
(7.4.57) |
合成波の強さ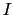 は,もとの波の強さを
は,もとの波の強さを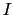
 ,
,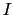
 とすると,(7.2.5),(7.4.3)式より,
とすると,(7.2.5),(7.4.3)式より,
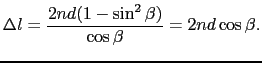 |
|
|
(7.4.58) |
となる.合成波の強さは,もとの波の強さの単純な和ではない.上式の右辺第3項を干渉項という.
次に,位相差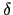 と薄膜の厚さ
と薄膜の厚さ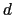 との関係を考えよう.A
との関係を考えよう.A BS
BS の経路で直接S
の経路で直接S に達する光と,ASTS
に達する光と,ASTS の経路をとる光とでは,
の経路をとる光とでは,
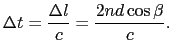 |
|
|
(7.4.59) |
の光路差がある.屈折の法則sin 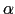 =
=  sin
sin 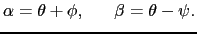 を用いると,
を用いると,
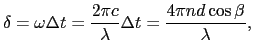 |
|
|
(7.4.60) |
したがって,S に達する時間差は,
に達する時間差は,
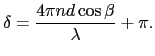 |
|
|
(7.4.61) |
こうして位相差は,
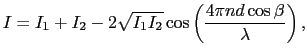 |
|
|
(7.4.62) |
となる.さらにS の反射は,屈折率の小さい媒質から大きい媒質に入射したときに相当するので,位相が
の反射は,屈折率の小さい媒質から大きい媒質に入射したときに相当するので,位相が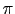 だけ変化することを考慮に入れて(7.2節),位相差は,
だけ変化することを考慮に入れて(7.2節),位相差は,
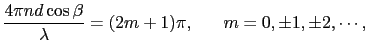 |
|
|
(7.4.63) |
(7.4.9)式を(7.4.4)式に代入すると,
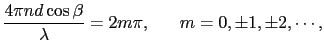 |
|
|
(7.4.64) |
となる.これより,反射光が最も明るくなるのは,
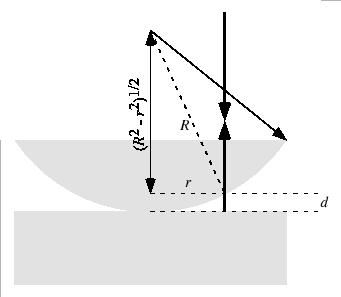 |
|
|
(7.4.65) |
が成り立つときである.最も暗くなるのは,
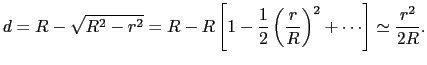 |
|
|
(7.4.66) |
が満たされるときである.
厚さがゆるやかに変化しているような場合にも光の干渉を観察できる.図7.13のように,曲率半径 の大きい平凸レンズを平面上にのせ,平面に垂直に光を当てると,接触点を中心として明暗の縞が同心円状に現れる.
の大きい平凸レンズを平面上にのせ,平面に垂直に光を当てると,接触点を中心として明暗の縞が同心円状に現れる.
これをニュートンリングという.このときは,レンズと平面の間に挟まれた空気が,薄膜の役目をする.接触点Oから の距離における膜の厚さは,
の距離における膜の厚さは,
![$\displaystyle d
=
R - \sqrt{R^{2} - r^{2}}
=
R - R \left [ 1 - {1 \over{2}} \left ( {r \over{R}} \right ) ^{2} + \cdots \right ]
\simeq
{r^{2} \over{2R}}.$](img1011.png) |
|
|
(7.4.67) |
垂直入射なので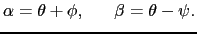 = 0,平面との反射による
= 0,平面との反射による の位相変化,空気の
の位相変化,空気の は1,なので,(7.4.11),(7.4.12)式から,
は1,なので,(7.4.11),(7.4.12)式から,
 |
|
|
(7.4.68) |
のとき明るく,
 |
|
|
(7.4.69) |
のとき暗くなることがわかる.
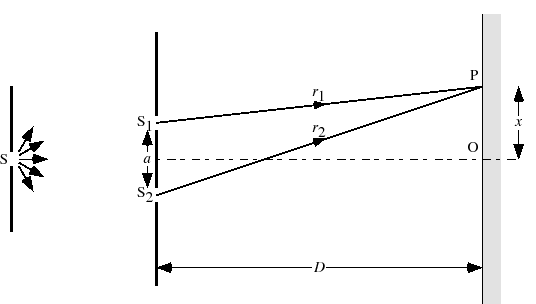
ヤングは,図7.14のように二つのピンホールを用いて,光の波面の分割による干渉実験を行った.
小さい孔Sを通った単色光がピンホールS ,S
,S に分かれてスクリーンに達する.ピンホールとスクリーン間の距離
に分かれてスクリーンに達する.ピンホールとスクリーン間の距離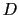 がピンホール相互の間隔
がピンホール相互の間隔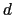 に比べて十分に大きいとすれば,(7.4.1)〜(7.4.3)式の関係が成り立つ.ここで,振幅
に比べて十分に大きいとすれば,(7.4.1)〜(7.4.3)式の関係が成り立つ.ここで,振幅
 ,
,
 は同一としてよい.位相差,
は同一としてよい.位相差,
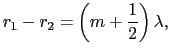 |
|
|
(7.4.70) |
は,
 -
- 
 が
が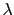 だけ変化したときに2
だけ変化したときに2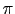 だけ変化する.したがって,
だけ変化する.したがって,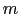 を整数として,
を整数として,
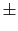 |
|
|
(7.4.71) |
のとき,強度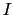 は極大で点Pは明るく,
は極大で点Pは明るく,
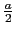 |
|
|
(7.4.72) |
のとき,強度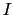 は極小で点Pは暗くなる.S
は極小で点Pは暗くなる.S S
S の垂直二等分線とスクリーンの交点をOとし,OP =
の垂直二等分線とスクリーンの交点をOとし,OP =  とすると,
とすると,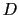
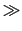

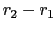
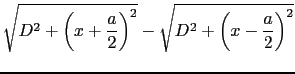 であるから,
であるから,
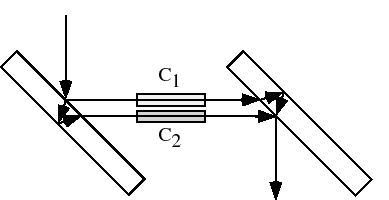
すなわち,スクリーン上では,Oを中心として,
 |
|
|
(7.4.74) |
のとき明るく,
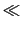 |
|
|
(7.4.75) |
のとき暗くなり,明暗が交互に並ぶことになる.



: 第15回演習問題
: 波動
: フェルマーの原理と幾何光学
Masashige Onoda
平成18年4月15日
![]() の物質でつくられた厚さ
の物質でつくられた厚さ![]() の一様な薄膜に,空気中から波長
の一様な薄膜に,空気中から波長![]() の光が入射角
の光が入射角![]() で入射する.
で入射する.
![]() やSBでは位相が等しくなっている.一方,A
やSBでは位相が等しくなっている.一方,A![]() からS
からS![]() へきてそこで反射される波と,AからTを経てS
へきてそこで反射される波と,AからTを経てS![]() から空気中へ出ていく波とでは,位相は異なる.
から空気中へ出ていく波とでは,位相は異なる.
![]() 軸をとり,両者とも正弦波で位相差を
軸をとり,両者とも正弦波で位相差を![]() とすると,
とすると,
![$\displaystyle f_{1}
=
A_{1} \sin {2\pi \over{\lambda}}(ct - x), \ \ \ \ \
f_{2}
=
A_{2} \sin \left [ {2\pi \over{\lambda}}(ct - x) + \delta \right ].$](img998.png)
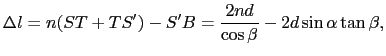
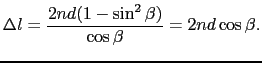
![]() と薄膜の厚さ
と薄膜の厚さ![]() との関係を考えよう.A
との関係を考えよう.A![]() BS
BS![]() の経路で直接S
の経路で直接S![]() に達する光と,ASTS
に達する光と,ASTS![]() の経路をとる光とでは,
の経路をとる光とでは,
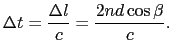
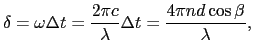
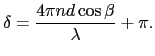
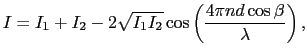
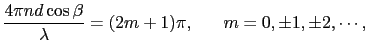
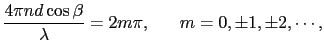

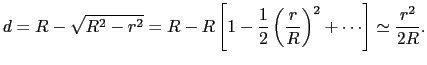
![]() の大きい平凸レンズを平面上にのせ,平面に垂直に光を当てると,接触点を中心として明暗の縞が同心円状に現れる.
の大きい平凸レンズを平面上にのせ,平面に垂直に光を当てると,接触点を中心として明暗の縞が同心円状に現れる.
![$\displaystyle d
=
R - \sqrt{R^{2} - r^{2}}
=
R - R \left [ 1 - {1 \over{2}} \left ( {r \over{R}} \right ) ^{2} + \cdots \right ]
\simeq
{r^{2} \over{2R}}.$](img1011.png)

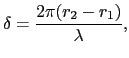
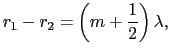
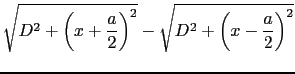 であるから,
であるから,
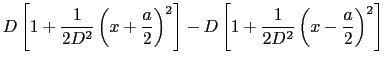
![$\displaystyle D \left [ 1 + {1 \over{2D^{2}}} \left ( x + {a \over{2}} \right )...
... D \left [ 1 + {1 \over{2D^{2}}} \left ( x - {a \over{2}} \right )^{2} \right ]$](img1023.png)