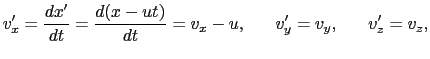: ローレンツ変換
: 特殊相対論への道
: 特殊相対論への道
宇宙船を月や火星に着陸させるのに成功したり,天体の運行を正確に予言したりできるのは,ニュートンの運動の法則が物体の運動を正確に記述するからである.しかし,ニュートンの運動の法則には適用限界がある.すなわち,光の速さに近い高速で運動する物体の運動の記述には,ニュートンの運動の法則は変更を要する.
一般に波動は媒質の振動が伝わるものである.電磁波である光の媒質は何であろうか?19世紀には,物質の存在しない真空中を波が伝わることは不合理と考え,宇宙のいたるところにエーテルという物質が充満していて,これを媒質として光が伝わると考えた.エーテルが存在するかどうかを検証した実験がマイケルソン-モーリーの実験であった.
エーテルを伝わる光の運動は川を走る船の運動にたとえられるだろう.
図8.1に示すように,流速0の上を速さ で動く船が,流速
で動く船が,流速 の川をくだるときは岸に対する速さは
の川をくだるときは岸に対する速さは +
+  で,川をさかのぼるときは
で,川をさかのぼるときは -
-  となる.この船が,ある地点から下流へ距離
となる.この船が,ある地点から下流へ距離 の地点まで1往復する時間
の地点まで1往復する時間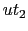 は,
は,
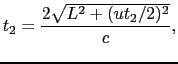 |
|
|
(8.1.1) |
次に,この船が幅 の川を1往復する時間を
の川を1往復する時間を
 とする.川は流速
とする.川は流速 で流れているので,船は対岸の
で流れているので,船は対岸の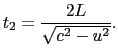 /2だけ上流の地点に向かうつもりで走ると,川の流れに垂直に進むことになる.したがって,
/2だけ上流の地点に向かうつもりで走ると,川の流れに垂直に進むことになる.したがって,
の関係が成り立つ.すなわち,
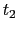 |
|
|
(8.1.2) |
このように川が流れていると,船が同じ距離を進む時間は進行方向によって異なる.
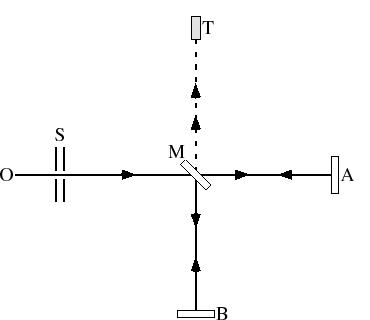
光の場合に上述のような時間の差があるかどうかを調べると,光の媒質があるかどうかがわかる.マイケルソンとモーリーは図8.2に示すような実験を行った.
図 8.2:
マイケルソン-モーリーの実験の概念図
|
|
- 光源Oからの光をスリットSで細い光線にする.
- 半透明の鏡Mで互いに垂直な2つの光線MAとMBに分け,鏡AとBで反射させる.
- 2つの反射光は鏡Mで反射あるいは透過して望遠鏡Tに入り,ここで干渉を起こし干渉縞をつくる.
- この装置は水銀の上に浮いているので,装置全体を水平面内で回転できる.装置を90度回転しても干渉縞はずれなかった.
地球は自転と公転を行っているので,慣性系に対して運動している.したがって,エーテルに対する地球の運動の効果が,(8.1.1)式の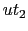 と(8.1.2)式の
と(8.1.2)式の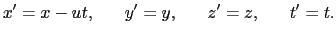 の差に対応する光波の位相の差になる.装置を90度回転すると
の差に対応する光波の位相の差になる.装置を90度回転すると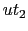 と
と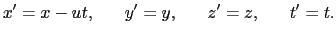 が入れ替わるので,位相差の変化が干渉縞のずれとして観測されるはずである.実験の結果,干渉縞のずれは1年のどの季節に観測しても検出されなかった.
が入れ替わるので,位相差の変化が干渉縞のずれとして観測されるはずである.実験の結果,干渉縞のずれは1年のどの季節に観測しても検出されなかった.
以上の実験から,真空中での光の速さの測定結果は,観測者の運動や光源の運動状態が変わっても,光の進む方向によらず一定であることになり,エーテルの存在は否定された.電磁波を伝える物質としての媒質はなく,宇宙空間でも電磁波を伝える電磁場は空間の性質,あるいは真空の性質だということになった.
光の速さはすべての慣性系でその進行方向によらず一定なので,光の速さの測定の立場からは特別な慣性系は存在しないことになった.すなわち,どの慣性系も他の慣性系に比べて優劣はつけられず,同等である.ニュートン力学では,ある慣性系に対して一定の速度で運動している座標系は慣性系であるというガリレイの相対性原理が成り立つ8.1.すなわち,一定の相対速度で運動している2つの慣性系では,同じ形の運動方程式が成り立つ.そこでアインシュタインは,次の二つの条件を物理学の基本原理と考えた(アインシュタインの相対性原理).
- ある慣性系に対して一定の速度で運動する座標系は慣性系である(特殊相対性原理).
- すべての慣性系で光の速さはその進行方向によらず一定である(光速度不変の原理).
この条件に基づく理論を特殊相対性理論という.
図8.3のように, 軸方向に一定の速さ
軸方向に一定の速さ の相対運動をしている2つの座標系O-
の相対運動をしている2つの座標系O-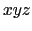 系(S系)とO
系(S系)とO -
-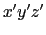 系(S
系(S 系)での座標の間には,ニュートン力学では,次の関係がある.
系)での座標の間には,ニュートン力学では,次の関係がある.
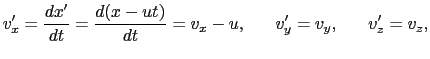 |
|
|
(8.1.3) |
2つの座標系での時間の測定に共通の時計を使えると考えるので,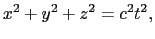 =
=  とおいた.(8.1.3)式から2つの座標系での速度
とおいた.(8.1.3)式から2つの座標系での速度 と
と
 との関係,
との関係,
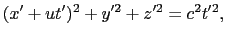 |
|
|
(8.1.4) |
すなわち,
 =
=  -
-  となる.しかし,この速度の関係から導かれる(8.1.1),(8.1.2)式を光の速度に適用すると,マイケルソン-モーリーの実験と矛盾する.(8.1.1),(8.1.2)式は日常生活で体験する現象では成り立つが,光や光のように速く動く物体の場合には成り立たない.
となる.しかし,この速度の関係から導かれる(8.1.1),(8.1.2)式を光の速度に適用すると,マイケルソン-モーリーの実験と矛盾する.(8.1.1),(8.1.2)式は日常生活で体験する現象では成り立つが,光や光のように速く動く物体の場合には成り立たない.



: ローレンツ変換
: 特殊相対論への道
: 特殊相対論への道
Masashige Onoda
平成18年4月15日
![\includegraphics[scale=1, clip]{fig-8-1-1.eps}](img1048.png)
 の地点まで1往復する時間
の地点まで1往復する時間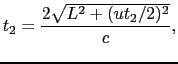
 の川を1往復する時間を
の川を1往復する時間を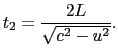 /2だけ上流の地点に向かうつもりで走ると,川の流れに垂直に進むことになる.したがって,
/2だけ上流の地点に向かうつもりで走ると,川の流れに垂直に進むことになる.したがって,
![]() 軸方向に一定の速さ
軸方向に一定の速さ![]() の相対運動をしている2つの座標系O-
の相対運動をしている2つの座標系O-![]() 系(S系)とO
系(S系)とO![]() -
-![]() 系(S
系(S![]() 系)での座標の間には,ニュートン力学では,次の関係がある.
系)での座標の間には,ニュートン力学では,次の関係がある.