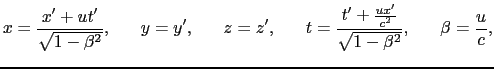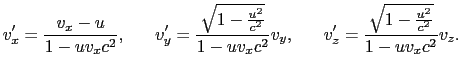: 同時刻の相対性
: 特殊相対論への道
: エーテル仮説とマイケルソン-モーリーの実験
ある瞬間S がSに原点も座標軸も一致したとし,そのとき光がSからみてすべての方向に
がSに原点も座標軸も一致したとし,そのとき光がSからみてすべての方向に という速度で伝わるとする.光の波面はSの原点Oを中心とする球面になるが,これは,
という速度で伝わるとする.光の波面はSの原点Oを中心とする球面になるが,これは,
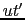 |
|
|
(8.2.5) |
で表される.この式をガリレイ変換によってS からみた記述に直せば,
からみた記述に直せば,
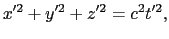 |
|
|
(8.2.6) |
となり,原点が-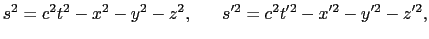 にある球面となる.しかし,実際には,
にある球面となる.しかし,実際には,
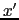 |
|
|
(8.2.7) |
が成り立たなければならない.いま,
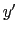 |
|
|
(8.2.8) |
とおこう.S,S は慣性系でどちらからみても他方は一定の速度で動くから,Sに対して一様な直線運動はS
は慣性系でどちらからみても他方は一定の速度で動くから,Sに対して一様な直線運動はS に対しても一様な直線運動でなければならない.すなわち,(
に対しても一様な直線運動でなければならない.すなわち,( ,
,  ,
,  ,
,  )についての1次の方程式は,(
)についての1次の方程式は,(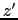 ,
, 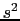 ,
, 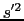 ,
, 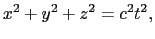 )についても1次の方程式でなければならない.したがって,(
)についても1次の方程式でなければならない.したがって,( ,
,  ,
,  ,
,  )と(
)と(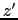 ,
, 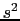 ,
, 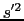 ,
, 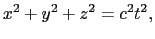 )との間の変換は1次変換でなければならない.
)との間の変換は1次変換でなければならない.
光速度不変の原理により,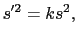 = 0ならば
= 0ならば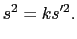 = 0で,その逆も成り立つから,
= 0で,その逆も成り立つから,
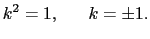 |
|
|
(8.2.9) |
の形でなければならない.ここでの定数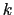 は(
は( ,
,  ,
,  ,
,  )にも(
)にも(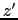 ,
, 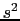 ,
, 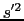 ,
, 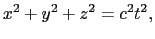 )にも依存しない.もし依存すると,場所と時刻によって空間・時間の性質が違うことになってしまう.また空間は方向性がないから
)にも依存しない.もし依存すると,場所と時刻によって空間・時間の性質が違うことになってしまう.また空間は方向性がないから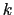 はS,S
はS,S の相対速度の方向にもよらない.相対性原理によればSに対して成り立つことはS
の相対速度の方向にもよらない.相対性原理によればSに対して成り立つことはS に対しても成り立つから,
に対しても成り立つから,
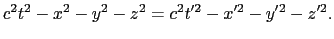 |
|
|
(8.2.10) |
(8.2.5),(8.2.6)式から,
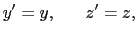 |
|
|
(8.2.11) |
 = 0の場合を考えれば
= 0の場合を考えれば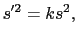 =
= 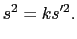 であるから,
であるから,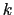 = 1でなければならない.このようにして,
= 1でなければならない.このようにして,
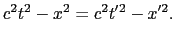 |
|
|
(8.2.12) |
こうして,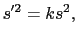 を不変に保つような1次変換を求めることになる.上で行った方法と同様の方法で,
を不変に保つような1次変換を求めることになる.上で行った方法と同様の方法で,
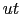 |
|
|
(8.2.13) |
が得られる.(8.2.8)式は,
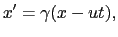 |
|
|
(8.2.14) |
S の原点O
の原点O (
(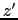 = 0)のSに対する運動は
= 0)のSに対する運動は =
= 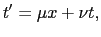 であるから,
であるから,
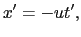 |
|
|
(8.2.15) |
でなければならない.変換のもう一つの式として,
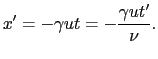 |
|
|
(8.2.16) |
とおく.
S からみたOの運動は,
からみたOの運動は,
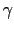 |
|
|
(8.2.17) |
で与えられると仮定しよう.一方,Oは = 0で与えられるから(8.2.11),(8.2.12)式より,
= 0で与えられるから(8.2.11),(8.2.12)式より,
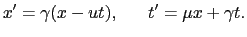 |
|
|
(8.2.18) |
これと(8.2.13)式とを比べて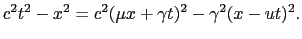 =
= 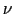 となる.それゆえ,
となる.それゆえ,
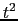 |
|
|
(8.2.19) |
これらを(8.2.10)式に代入して,
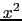 |
|
|
(8.2.20) |
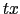 ,
,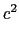 ,
,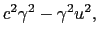 の係数を比較して,
の係数を比較して,
上の第1,第3式から,
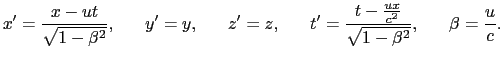 |
|
|
(8.2.21) |
が得られる.
 = 0で
= 0で
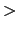 0に対して
0に対して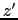
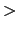 0になるように
0になるように ,
,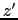 をとると
をとると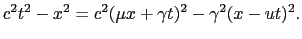
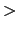 0でなければならない.したがって,
0でなければならない.したがって,
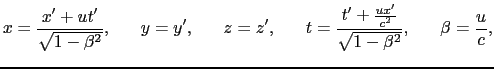 |
|
|
(8.2.22) |
これで( ,
,  ,
,  ,
,  )と(
)と(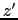 ,
, 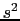 ,
, 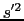 ,
, 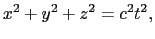 )の関係を与える変換の式が得られた.
)の関係を与える変換の式が得られた.
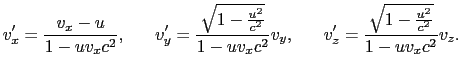 |
|
|
(8.2.23) |
これらを ,
, ,
, ,
, につき解いて,
につき解いて,
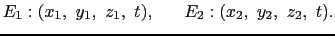 |
|
|
(8.2.24) |
が得られる.(8.2.19),(8.2.20)式をローレンツ変換と呼ぶ8.2.これらの式で
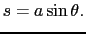
 とすればガリレイの変換が得られる.(8.2.19),(8.2.20)式から導かれるS系での速度
とすればガリレイの変換が得られる.(8.2.19),(8.2.20)式から導かれるS系での速度 とS
とS 系での速度
系での速度
 の関係は,
の関係は,
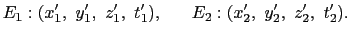 |
|
|
(8.2.25) |



: 同時刻の相対性
: 特殊相対論への道
: エーテル仮説とマイケルソン-モーリーの実験
Masashige Onoda
平成18年4月15日
![]() = 0ならば
= 0ならば![]() = 0で,その逆も成り立つから,
= 0で,その逆も成り立つから,
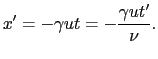
![]() からみたOの運動は,
からみたOの運動は,
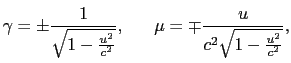
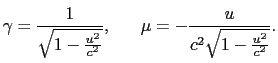
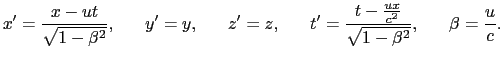
![]() = 0で
= 0で![]()
![]() 0に対して
0に対して![]()
![]() 0になるように
0になるように![]() ,
,![]() をとると
をとると![]()
![]() 0でなければならない.したがって,
0でなければならない.したがって,