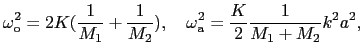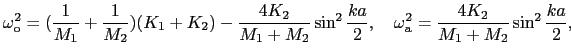: アインシュタインモデルとデバイモデル
: 格子振動とフォノン
: 1種類の原子からなる1次元格子
目次
2種類の原子の質量 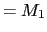 (奇数),
(奇数),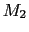 (偶数)
バネ定数と原子間距離
(偶数)
バネ定数と原子間距離 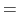 交互に
交互に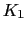 ,
,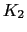 ,
,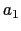 ,
,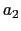 格子定数
格子定数
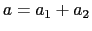
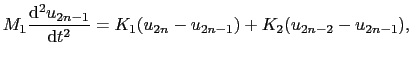 |
|
|
(2.1.9) |
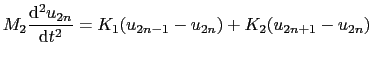 |
|
|
(2.1.10) |
ここで
![$\displaystyle u_{2n-1} = A_{1}{\rm exp}[{\rm i}[k(n - 1)a - \omega t],\ \ \ u_{2n} = A_{2}{\rm exp}[{\rm i}[k((n - 1)a + a_{1}) - \omega t],$](img171.png) |
|
|
(2.1.11) |
を代入すると
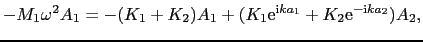 |
|
|
(2.1.12) |
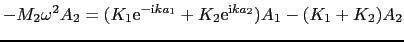 |
|
|
(2.1.13) |
したがって
![$\displaystyle \omega^{2} = {1 \over{2}}[{M_{1} + M_{2} \over{M_{1}M_{2}}}(K_{1}...
...} + K_{2})^{2} - {16K_{1}K_{2} \over{M_{1}M_{2}}}\sin^{2}{ka \over{2}}]^{1/2}],$](img174.png) |
|
|
(2.1.14) |
(2-8)式について,以下の2つの場合を考察してみよう.
-
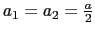 ,
,
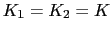 の場合
の場合
![$\displaystyle \omega^{2} = ({1 \over{M_{1}}} + {1 \over{M_{2}}})K \pm K[({1 \ov...
...}} + {1 \over{M_{2}}})^{2} - {4 \over{M_{1}M_{2}}\sin^{2}{ka \over{2}}}]^{1/2},$](img177.png) |
|
|
(2.1.15) |
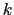 が小さいときは(2-9)式を展開して
が小さいときは(2-9)式を展開して
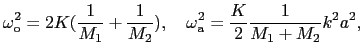 |
|
|
(2.1.16) |
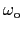 →光学モード(optical mode)
→光学モード(optical mode)
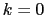 のとき,
のとき,
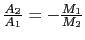
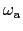 →音響モード(acoustic mode);長波長での弾性波
→音響モード(acoustic mode);長波長での弾性波
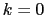 のとき,
のとき,
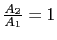
表 2.1:
光学モード,音響モードの原子運動
| |
|
○ |
● |
○ |
● |
○ |
● |
○ |
● |
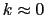 |
ac |
→ |
→ |
→ |
→ |
→ |
→ |
→ |
→ |
| |
op |
→ |
← |
→ |
← |
→ |
← |
→ |
← |
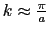 |
ac |
→ |
→ |
← |
← |
→ |
→ |
← |
← |
| |
op |
→ |
← |
← |
→ |
→ |
← |
← |
→ |
-
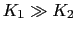 の場合;分子結合物質に対応するモデル
の場合;分子結合物質に対応するモデル
(2-8)式を
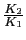 で展開する.
で展開する.
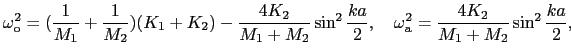 |
|
|
(2.1.17) |
o→分子内振動から派生したもの.
a→分子内では変位しない原子が弱いバネ定数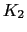 で結ばれているように振る舞う.
で結ばれているように振る舞う.




: アインシュタインモデルとデバイモデル
: 格子振動とフォノン
: 1種類の原子からなる1次元格子
目次
Masashige Onoda
平成18年4月7日
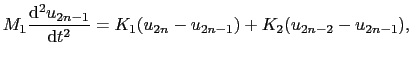
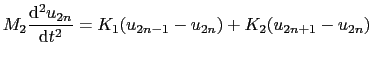
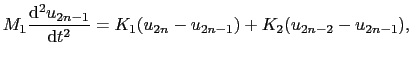
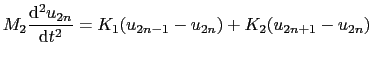
![$\displaystyle \omega^{2} = {1 \over{2}}[{M_{1} + M_{2} \over{M_{1}M_{2}}}(K_{1}...
...} + K_{2})^{2} - {16K_{1}K_{2} \over{M_{1}M_{2}}}\sin^{2}{ka \over{2}}]^{1/2}],$](img174.png)
![$\displaystyle \omega^{2} = ({1 \over{M_{1}}} + {1 \over{M_{2}}})K \pm K[({1 \ov...
...}} + {1 \over{M_{2}}})^{2} - {4 \over{M_{1}M_{2}}\sin^{2}{ka \over{2}}}]^{1/2},$](img177.png)