: 超伝導と遷移金属酸化物
: BCS理論
: ボゴリューボフ変換による解
目次
ボゴリューボフ変換を用いて
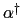 ,
,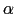 を定義し,
を定義し,
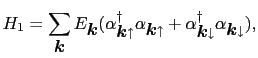 |
|
|
(7.11.122) |
を考える.次に,
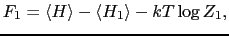 |
|
|
(7.11.123) |
を最小にするように,(7.11.42)式の
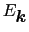 と(7.11.29)式の
と(7.11.29)式の
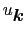 ,
,
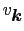 を決定する.これは有限温度のハートリーフォック近似を意味する7.2.
を決定する.これは有限温度のハートリーフォック近似を意味する7.2.
![$\displaystyle Z_{1} = {\rm Tr} [ \exp (-\beta H_{1}) ] = \prod_{\mbox{\boldmath$k$}} \left [ 1 + \exp (-\beta E_{\mbox{\boldmath$k$}}) \right ] ^{2},$](img1532.png) |
|
|
(7.11.124) |
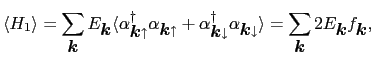 |
|
|
(7.11.125) |
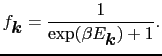 |
|
|
(7.11.126) |
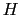 は(7.11.31)式のように表されているが,
は(7.11.31)式のように表されているが,
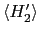 = 0,
= 0,
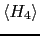 =
=
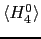 であり,
であり,
![$\displaystyle \langle H_{2} \rangle = 2\sum_{\mbox{\boldmath$k$}} [ \epsilon_{\...
...\,' u_{\mbox{\boldmath$k$}'}v_{\mbox{\boldmath$k$}'} ] f_{\mbox{\boldmath$k$}},$](img1538.png) |
|
|
(7.11.127) |
![$\displaystyle \langle H_{4}^{(0)} \rangle = -V\sum_{\mbox{\boldmath$k$}}\,' \su...
...v_{\mbox{\boldmath$k$}'}^{2}) ] f_{\mbox{\boldmath$k$}}f_{\mbox{\boldmath$k$}'}$](img1539.png) |
|
|
(7.11.128) |
である.これらを(7.11.43)式に代入する.
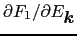 = 0より,
= 0より,
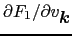 = 0より,
= 0より,
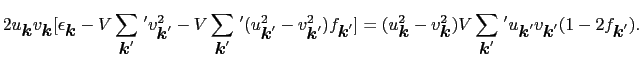 |
|
|
(7.11.130) |
(7.11.49),(7.11.50)式の左辺の括弧内で
を無視すると,(7.11.50)式の解は,
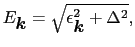 |
|
|
(7.11.131) |
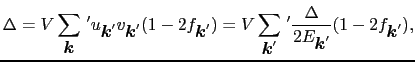 |
|
|
(7.11.132) |
となる.(7.11.52)式をギャップ方程式と呼ぶ.
ギャップ方程式について調べよう.状態密度をフェルミ面での値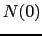 で近似すると,
で近似すると,
![$\displaystyle {1 \over{N(0)V}} = \int_{0}^{\hbar\omega_{\rm c}} {{\rm d}\epsilo...
...}}}} \tanh \left [ {1 \over{2}}\beta \sqrt{\epsilon^{2} + \Delta^{2}} \right ],$](img1549.png) |
|
|
(7.11.133) |
となる.(7.11.53)式から決まる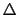 は,
は,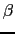 ,すなわち温度
,すなわち温度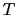 によって変化する.tanhの項は
によって変化する.tanhの項は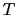 が増加すると減少するので,(7.11.53)式から決まる
が増加すると減少するので,(7.11.53)式から決まる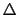 は温度が増加すると単調に減少する.
は温度が増加すると単調に減少する.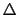 = 0になる温度が
= 0になる温度が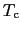 である.すなわち,
である.すなわち,
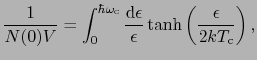 |
|
|
(7.11.134) |
から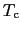 は決定される.部分積分すると,
は決定される.部分積分すると,
![$\displaystyle {1 \over{N(0)V}} = [ \log x \tanh x ]_{0}^{{\hbar\omega_{\rm c} \...
...0}^{{\hbar\omega_{\rm c} \over{2kT_{\rm c}}}} {\rm d}x \log x {\rm sech}^{2} x,$](img1551.png) |
|
|
(7.11.135) |
を得る.ここで
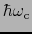
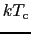 より,
より,
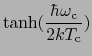
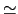 1と近似できるから,
1と近似できるから,
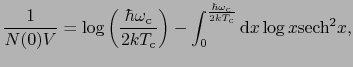 |
|
|
(7.11.136) |
となる.さらに上式第2項の積分の上限を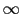 に置き換えると,
に置き換えると,
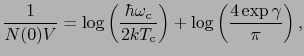 |
|
|
(7.11.137) |
を得る.ここで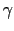 はオイラー定数である.こうして,
はオイラー定数である.こうして,
となる.(7.11.57),(7.11.19)式より,
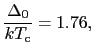 |
|
|
(7.11.139) |
が導かれる.実験によれば,
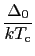 = 3.0 - 4.5である.
= 3.0 - 4.5である.




: 超伝導と遷移金属酸化物
: BCS理論
: ボゴリューボフ変換による解
目次
Masashige Onoda
平成18年4月7日
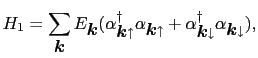
![]() で近似すると,
で近似すると,