


: 装置の起動方法
: 電磁石の特性
: 実験装置の回路配線
目次
磁場分布はホール素子を用いたガウスメーターで測定する.ホール素子は壊れやすいので特に注意して取り扱うようにする.
ホール素子とは,ローレンツ力によるホール(Hall)効果を利用した磁場測定用の素子である.ホール効果実験は図9のように行われる.
電場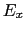 は
は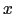 方向に伸びた伝導体にかかり,電流密度
方向に伸びた伝導体にかかり,電流密度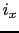 が流れている.磁場
が流れている.磁場
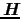 は正の
は正の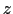 方向にかかっている.このときローレンツ力
方向にかかっている.このときローレンツ力
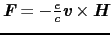 が働く.このために電子は負の
が働く.このために電子は負の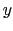 方向に偏る.電子がそこにたまるにつれて,電子の運動とその蓄積を妨げるように
方向に偏る.電子がそこにたまるにつれて,電子の運動とその蓄積を妨げるように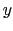 方向に電場ができる.平衡状態では,横電場
方向に電場ができる.平衡状態では,横電場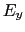 はローレンツ力とつり合い,電流は
はローレンツ力とつり合い,電流は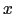 方向にのみ流れる.すなわち
方向にのみ流れる.すなわち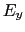 は磁場
は磁場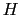 と電流
と電流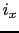 に比例する.ここで
に比例する.ここで
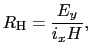 |
|
|
(2.13) |
で定義される量をホール係数と呼ぶ.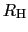 の符号により電荷の符号を決めることができる.
の符号により電荷の符号を決めることができる.
もう少し詳しく見てみよう.任意の成分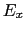 ,
,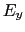 を持つ電場と,
を持つ電場と,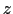 軸に沿った磁場
軸に沿った磁場
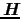 とがかかっている場合の電流密度
とがかかっている場合の電流密度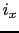 ,
,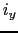 を求める.電子1個当りの運動方程式は,
を求める.電子1個当りの運動方程式は,
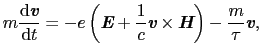 |
|
|
(2.14) |
となる.ここで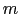 は電子の質量,
は電子の質量,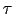 は緩和時間を表す.定常状態では,
は緩和時間を表す.定常状態では,
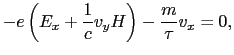 |
|
|
(2.15) |
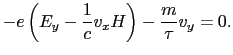 |
|
|
(2.16) |
単位体積中の自由電子数を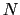 とし,上式の両辺に
とし,上式の両辺に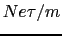 をかけ,
をかけ,
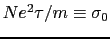 ,
,
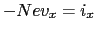 という関係を用いると,
という関係を用いると,
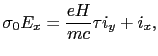 |
|
|
(2.17) |
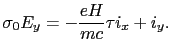 |
|
|
(2.18) |
ここで横電流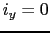 とおけば,
とおけば,
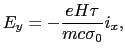 |
|
|
(2.19) |
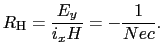 |
|
|
(2.20) |
今の場合は,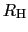 を既知とし,測定系の定電流値と測定電圧値をもとに磁場を求めている.
を既知とし,測定系の定電流値と測定電圧値をもとに磁場を求めている.



: 装置の起動方法
: 電磁石の特性
: 実験装置の回路配線
目次
Masashige Onoda
平成18年4月7日
![]() は
は![]() 方向に伸びた伝導体にかかり,電流密度
方向に伸びた伝導体にかかり,電流密度![]() が流れている.磁場
が流れている.磁場
![]() は正の
は正の![]() 方向にかかっている.このときローレンツ力
方向にかかっている.このときローレンツ力
![]() が働く.このために電子は負の
が働く.このために電子は負の![]() 方向に偏る.電子がそこにたまるにつれて,電子の運動とその蓄積を妨げるように
方向に偏る.電子がそこにたまるにつれて,電子の運動とその蓄積を妨げるように![]() 方向に電場ができる.平衡状態では,横電場
方向に電場ができる.平衡状態では,横電場![]() はローレンツ力とつり合い,電流は
はローレンツ力とつり合い,電流は![]() 方向にのみ流れる.すなわち
方向にのみ流れる.すなわち![]() は磁場
は磁場![]() と電流
と電流![]() に比例する.ここで
に比例する.ここで
![]() ,
,![]() を持つ電場と,
を持つ電場と,![]() 軸に沿った磁場
軸に沿った磁場
![]() とがかかっている場合の電流密度
とがかかっている場合の電流密度![]() ,
,![]() を求める.電子1個当りの運動方程式は,
を求める.電子1個当りの運動方程式は,