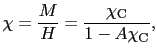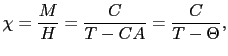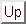


: 高温超伝導
: 相転移
: 相転移
目次
前回はスピン間の相互作用が比較的小さい物質系を対象とした.今回は,スピン間の相互作用が強い場合の現象の一例として金属Gdの磁化の温度変化を測定する.Gdは室温近傍で強磁性状態に転移する.
常磁性-強磁性転移あるいは相転移などの現象は,本質的に相互作用の存在による.この種の問題を厳密に取り扱うことは難しいが,いくつかの近似的な考え方によって現象の本質をつかむことができる.相互作用を持つ多数のスピンからなる系を取り扱う場合,一つの近似として次のように考える.一つのスピンに注目し,他のスピンからそれにおよぼされる作用は平均的に定まるある力場2として,そのスピンに働くものとし,その平均力場,いわゆる分子場の中での一つのスピンを統計力学的に取り扱う.その取り扱いから,逆にこのスピンが他のスピンにおよぼす平均力場を定めることができるが,スピンが同等であるならば,この平均力場はさきに仮定されたものに同等でなければならない.このつじつまを合せる要求から,分子場が定まり,これにより系の統計的性質が定められる.
いま外から磁場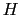 を作用させる.一つのスピンに働く力はこの磁場の他に周囲のスピンとの相互作用によるものがある.これを平均的に考え,ある磁場
を作用させる.一つのスピンに働く力はこの磁場の他に周囲のスピンとの相互作用によるものがある.これを平均的に考え,ある磁場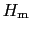 に等価なものとして作用すると仮定する.この仮定によれば一つのスピンに働く有効磁場
に等価なものとして作用すると仮定する.この仮定によれば一つのスピンに働く有効磁場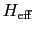 は,
は,
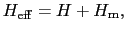 |
|
|
(7.25) |
と書ける.もし磁化がなければ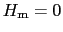 であるから,
であるから,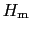 は磁化の大きさ
は磁化の大きさ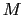 に比例すると仮定しよう.
に比例すると仮定しよう.
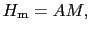 |
|
|
(7.26) |
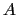 を分子場係数と呼ぶ.相互作用がないときのスピンの帯磁率はキュリー型帯磁率
を分子場係数と呼ぶ.相互作用がないときのスピンの帯磁率はキュリー型帯磁率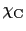 で与えられるから,磁化は,
で与えられるから,磁化は,
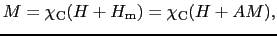 |
|
|
(7.27) |
と表される.したがって帯磁率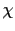 は,
は,
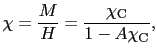 |
|
|
(7.28) |
となる.
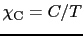 を用いれば,
を用いれば,
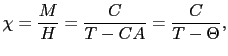 |
|
|
(7.29) |
を得る.これがキュリーワイス型の帯磁率である.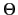 を特にワイス温度と呼ぶ.
を特にワイス温度と呼ぶ.
ガドリニウムGdに対して5節の1〜5を行う.
Masashige Onoda
平成18年4月7日
![]() を作用させる.一つのスピンに働く力はこの磁場の他に周囲のスピンとの相互作用によるものがある.これを平均的に考え,ある磁場
を作用させる.一つのスピンに働く力はこの磁場の他に周囲のスピンとの相互作用によるものがある.これを平均的に考え,ある磁場![]() に等価なものとして作用すると仮定する.この仮定によれば一つのスピンに働く有効磁場
に等価なものとして作用すると仮定する.この仮定によれば一つのスピンに働く有効磁場![]() は,
は,