- ...table:naiyouに掲げる磁気的性質を定量的に知ることを目的とする1
- 実験室1F101,連絡先:TA(Tel 4035,4352);小野田(Tel 4236,onoda@sakura.cc.tsukuba.ac.jp)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...常磁性-強磁性転移あるいは相転移などの現象は,本質的に相互作用の存在による.この種の問題を厳密に取り扱うことは難しいが,いくつかの近似的な考え方によって現象の本質をつかむことができる.相互作用を持つ多数のスピンからなる系を取り扱う場合,一つの近似として次のように考える.一つのスピンに注目し,他のスピンからそれにおよぼされる作用は平均的に定まるある力場2
- 本当は他のスピンの状態に依存し,さまざまの値を確率的にとる.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...の値は,一般には自由電子のそれとは異なり2.0023からずれることが多い3
- 周りのイオンからの結晶場やスピン軌道相互作用が,電子のエネルギー準位に影響を与えるからである.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...nigd-a).この構造では,各原子は12個の等距離の最近接原子に囲まれている4
- 面心立方構造はまた,原点がそれぞれ
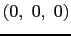 ,
,
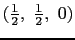 ,
,
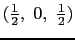 ,
,
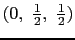 にある同じ格子定数を持つ四つの単純立方構造を組み合わせた構造であるとも考えることができる.
にある同じ格子定数を持つ四つの単純立方構造を組み合わせた構造であるとも考えることができる.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...歳差運動5
- 歳差運動の他の例としては,重力場におけるこまの回転運動が知られている.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
となる.ここで右辺の第2項6
- この効果を分極効果という.量子論的にいえば,摂動項
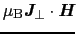 によって,磁場のないときの基底状態の
によって,磁場のないときの基底状態の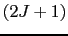 重に縮退した波動関数に,励起状態が混ざってくることである.詳細は文献[ref3]を参照のこと.一方,
重に縮退した波動関数に,励起状態が混ざってくることである.詳細は文献[ref3]を参照のこと.一方,
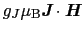 の効果を配向効果と呼ぶことがある.
の効果を配向効果と呼ぶことがある.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
である7
- 量子力学的な固有状態で
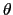 がはっきり一定値をとるわけではなく,
がはっきり一定値をとるわけではなく,
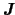 の成分
の成分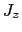 の期待値が
の期待値が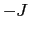 から
から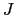 までの
までの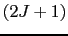 個の値のいずれかをとる.
個の値のいずれかをとる.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...交換相互作用8
- 交換相互作用が水素分子の結合エネルギーに本質的役割を演じることは,ハイトラーロンドンの理論として知られている.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...は種々の波動関数に対する平均とする9
- (B.36)式の形の相互作用はハイゼンベルグの考えたような直接交換相互作用だけでなく,もっと複雑な機構によっても現れる.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...が小さくても有限の物質では,十分温度を下げれば常磁性状態はたいてい強磁性をはじめとするスピンの秩序状態に移行する.実際の強磁性体では外部磁場をかけないときは磁化はゼロであるが,非常に小さい磁場で容易に飽和値まで磁化される.これは,強磁性体内では自発磁化を持っている小区域が多数あって,外部磁場のないときには小区域ごとに自発磁化の方向が異なっており,全体としてみれば各小区域の磁化が打ち消し合っているためである10
- 磁場ゼロでも試料全体で準安定的にスピンが一様に揃って磁化を持っている物質が永久磁石である.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...バナジウム酸化物11
- 高温超伝導酸化物の超伝導発現機構や種々の低次元スピンネットワークを持つ
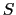 =
= 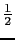 系の構造・物性の解明は,物性物理学研究における最重要課題の一つである.
系の構造・物性の解明は,物性物理学研究における最重要課題の一つである.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...eq-5420)式にほぼ従う12
- 図22(a)および図22(b)の実線は,より進んだモデルに基づく計算結果である.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...これら二つの角運動量が物質の磁気的性質を担い,磁気モーメント13
- 実は,原子核も磁気モーメントを持っているが,それは小さく普通にいう磁性の中には入ってこない.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...eq-1080)式の第2項のみである14
- (2.4)式を用いれば,この項に起因する帯磁率は,
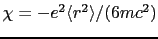 となる.
となる.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.