


: 磁気共鳴理論
: 常磁性・強磁性理論
: 常磁性,強磁性の分子場理論とキュリーワイスの法則
目次
常磁性体やただし磁化の方向や大きさは物質によって異なる.前に「鉄は磁場の方向に強く磁化され銅は磁化されない.」と述べたが,実際には「銅は磁場と反対の方向にごく僅か磁化されている.」と言ったほうがよい.鉄のような性質を持つ物質は強磁性体と呼ばれ,銅は反磁性体と呼ばれる.一般に反磁性体の磁化の絶対値は鉄のそれに比べて非常に小さく,たとえば10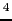 [G (ガウス)](1 [T])の磁場の下では,鉄の磁化の大きさの数十万分の1程度である.磁石に引きつけられる性質を持つ物質の中には,磁化の大きさが強磁性体に比べて桁違いに小さく,また磁化が磁場に比例していて,磁場がないときには,磁化が必ずゼロであるようなものがある.この性質は常磁性と呼ばれ,強磁性と区別される.強磁性体の温度を上げていくと,ある温度以上では常磁性を示すようになる.
この他にも様々な磁性体が存在するがここでは省略する.
[G (ガウス)](1 [T])の磁場の下では,鉄の磁化の大きさの数十万分の1程度である.磁石に引きつけられる性質を持つ物質の中には,磁化の大きさが強磁性体に比べて桁違いに小さく,また磁化が磁場に比例していて,磁場がないときには,磁化が必ずゼロであるようなものがある.この性質は常磁性と呼ばれ,強磁性と区別される.強磁性体の温度を上げていくと,ある温度以上では常磁性を示すようになる.
この他にも様々な磁性体が存在するがここでは省略する.
強磁性,常磁性あるいは反磁性などの性質は,「原子が磁気モーメントを持つか否か?」に関係づけられる.原子を構成する電子の運動は,原子核の正電荷と他の電子の負電荷によるクーロン力で支配される.一つの電子に着目し他の電子の分布を平均化して考えると,一つ一つの電子はある球対称なポテンシャルの中を動くとみなされるだろう.量子力学によれば,この電子の運動は主量子数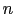 と方位量子数
と方位量子数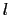 とで指定される状態になる.その各々は殻と呼ばれ,電子はパウリ原理に従ってエネルギーの低い状態から順にこの殻を埋める.
とで指定される状態になる.その各々は殻と呼ばれ,電子はパウリ原理に従ってエネルギーの低い状態から順にこの殻を埋める.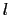
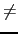 0の殻にある電子は,原子核のまわりで回転運動を行うことによる軌道角運動量
0の殻にある電子は,原子核のまわりで回転運動を行うことによる軌道角運動量
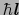 を持つ.この他に電子は自転による固有のスピン角運動量
を持つ.この他に電子は自転による固有のスピン角運動量
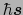 を持つ.
を持つ.
これら二つの角運動量が物質の磁気的性質を担い,磁気モーメント13と関係づけられる.
一方,軌道運動に伴う磁気モーメントは「電子の電荷」 「電子の運動の面積速度」で与えられるので,
「電子の運動の面積速度」で与えられるので,
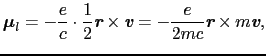 |
|
|
(B..89) |
となる.磁場がない場合には,
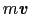 は運動量
は運動量
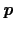 に等しいので,
に等しいので,
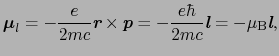 |
|
|
(B..90) |
とおける.一方磁場がある場合には,
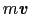 は
は
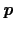 とベクトルポテンシャル
とベクトルポテンシャル
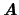 を用いて,
を用いて,
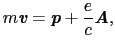 |
|
|
(B..91) |
と表されるので,
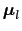 は,
は,
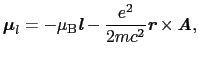 |
|
|
(B..92) |
となる.ここで,
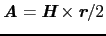 とおくと,
とおくと,
![$\displaystyle \mbox{\boldmath$\mu$}_{l} = - \mu_{\rm B} \mbox{\bfseries\itshape...
...itshape {r}} \cdot \mbox{\bfseries\itshape {H}}) \mbox{\bfseries\itshape {r}}],$](img375.png) |
|
|
(B..93) |
を得る.第1項の軌道角運動量
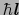 は,大きさが
は,大きさが
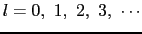 の
の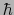 倍で,これらの固有軌道はそれぞれ
倍で,これらの固有軌道はそれぞれ
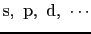 と呼ばれる.第2項は,磁場によって誘起される磁気モーメントで,その本質はレンツの法則に基づいている.軌道運動磁気モーメントは磁場の大きさに依存するので,磁場との相互作用のエネルギーは
と呼ばれる.第2項は,磁場によって誘起される磁気モーメントで,その本質はレンツの法則に基づいている.軌道運動磁気モーメントは磁場の大きさに依存するので,磁場との相互作用のエネルギーは
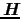 で積分して,
で積分して,
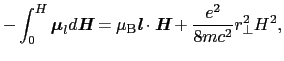 |
|
|
(B..94) |
となる. は電子の原子核から測った位置ベクトル
は電子の原子核から測った位置ベクトル
 の磁場に垂直な成分を表す.
の磁場に垂直な成分を表す.
原子の磁気モーメントの有無は,個々の電子の磁気モーメントの配列の仕方などに依存することが期待される.強磁性体は,構成原子の中に磁気モーメントを持つものがあって,しかもそれらの磁気モーメントがすべてある方向に揃っている物質である.常磁性状態では,磁場がない場合には個々の電子の磁気モーメントが無秩序な配列をとるが,磁場がかかると一つの磁気モーメントが磁場の方向を向く確率が他の方向を向く確率よりも僅かに増加し,全体として僅かに磁場方向に磁化された状態が実現する.反磁性状態は,たとえば閉殻原子で実現する.閉殻の場合,すべての電子のスピンの和および軌道角運動量の和はゼロであるので,原子の磁気モーメントは(B.59)式の第2項のみである14.
Masashige Onoda
平成18年4月7日
![]() と方位量子数
と方位量子数![]() とで指定される状態になる.その各々は殻と呼ばれ,電子はパウリ原理に従ってエネルギーの低い状態から順にこの殻を埋める.
とで指定される状態になる.その各々は殻と呼ばれ,電子はパウリ原理に従ってエネルギーの低い状態から順にこの殻を埋める.![]()
![]() 0の殻にある電子は,原子核のまわりで回転運動を行うことによる軌道角運動量
0の殻にある電子は,原子核のまわりで回転運動を行うことによる軌道角運動量
![]() を持つ.この他に電子は自転による固有のスピン角運動量
を持つ.この他に電子は自転による固有のスピン角運動量
![]() を持つ.
を持つ.
![]() 「電子の運動の面積速度」で与えられるので,
「電子の運動の面積速度」で与えられるので,