


: 金属酸化物から
: 結晶構造
: 結晶構造
目次
Cu,Ni,Ptなどは立方晶,空間群
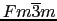 (No. 225)に属し,面心立方構造をとる.Ni,Ptの格子定数はそれぞれ
(No. 225)に属し,面心立方構造をとる.Ni,Ptの格子定数はそれぞれ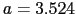 ,3.923 [Å]である.名前が示すように原子は立方体の隅の他に面の中心にも位置しており,単位格子は4個の原子を
,3.923 [Å]である.名前が示すように原子は立方体の隅の他に面の中心にも位置しており,単位格子は4個の原子を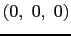 ,
,
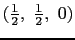 ,
,
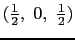 ,
,
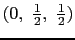 に持っている(図16(a)).この構造では,各原子は12個の等距離の最近接原子に囲まれている4.面心立方構造は立方最密充填構造とも呼ばれ,単位格子を
に持っている(図16(a)).この構造では,各原子は12個の等距離の最近接原子に囲まれている4.面心立方構造は立方最密充填構造とも呼ばれ,単位格子を
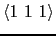 方向に沿って眺めると立方の最密充填層が認められる.
方向に沿って眺めると立方の最密充填層が認められる.
Gdなど多くの希土類元素や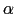 型Tiは六方晶,空間群
型Tiは六方晶,空間群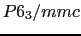 (No. 194)に属し,六方最密充填構造をとる.六方単位格子の形は図16(b)に示すように
(No. 194)に属し,六方最密充填構造をとる.六方単位格子の形は図16(b)に示すように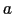 軸と
軸と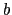 軸との間の角度が120
軸との間の角度が120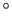 ,
,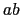 面と
面と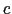 軸との間の角度は90
軸との間の角度は90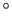 であり,Gdでは,
であり,Gdでは,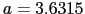 ,
,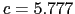 [Å],Tiでは,
[Å],Tiでは,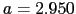 ,
,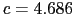 [Å]である.六方最密充填構造の単位格子では,1個の原子が
[Å]である.六方最密充填構造の単位格子では,1個の原子が
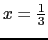 ,
,
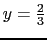 の線上の高さが単位格子の
の線上の高さが単位格子の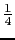 の位置に,他の1個の原子が
の位置に,他の1個の原子が
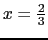 ,
,
 の線上の高さが単位格子の
の線上の高さが単位格子の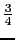 の位置にある.したがって原子は単位格子内の
の位置にある.したがって原子は単位格子内の
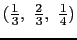 および
および
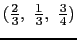 を占める.六方最密充填構造では面心立方構造と同様にそれぞれの原子は12個の最近接原子で囲まれている.
=0pt
を占める.六方最密充填構造では面心立方構造と同様にそれぞれの原子は12個の最近接原子で囲まれている.
=0pt
図 16:
NiおよびGdの結晶構造
[Niの結晶構造(単位胞)] ![\includegraphics[height=4.2cm]{nicv5.eps}](img215.png)
[Gdの結晶構造] ![\includegraphics[height=4.2cm]{gdcv5.eps}](img216.png)
|
Masashige Onoda
平成18年4月7日
![]() 型Tiは六方晶,空間群
型Tiは六方晶,空間群![]() (No. 194)に属し,六方最密充填構造をとる.六方単位格子の形は図16(b)に示すように
(No. 194)に属し,六方最密充填構造をとる.六方単位格子の形は図16(b)に示すように![]() 軸と
軸と![]() 軸との間の角度が120
軸との間の角度が120![]() ,
,![]() 面と
面と![]() 軸との間の角度は90
軸との間の角度は90![]() であり,Gdでは,
であり,Gdでは,![]() ,
,![]() [Å],Tiでは,
[Å],Tiでは,![]() ,
,![]() [Å]である.六方最密充填構造の単位格子では,1個の原子が
[Å]である.六方最密充填構造の単位格子では,1個の原子が
![]() ,
,
![]() の線上の高さが単位格子の
の線上の高さが単位格子の![]() の位置に,他の1個の原子が
の位置に,他の1個の原子が
![]() ,
,
![]() の線上の高さが単位格子の
の線上の高さが単位格子の![]() の位置にある.したがって原子は単位格子内の
の位置にある.したがって原子は単位格子内の
![]() および
および
![]() を占める.六方最密充填構造では面心立方構造と同様にそれぞれの原子は12個の最近接原子で囲まれている.
=0pt
を占める.六方最密充填構造では面心立方構造と同様にそれぞれの原子は12個の最近接原子で囲まれている.
=0pt