


: 自由ラジカルの電子スピン共鳴
: ミクロな測定手段
: ミクロな測定手段
目次
磁場
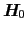 中での磁気モーメント
中での磁気モーメント
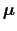 のエネルギーは,2.1節で議論したように,
のエネルギーは,2.1節で議論したように,
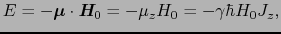 |
|
|
(9.32) |
である.ここで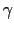 は磁気回転比で
は磁気回転比で
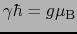 である.
である.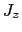 のとりうる値は,
のとりうる値は,
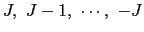 である.これをゼーマン準位と呼ぶ.隣り合う準位間のエネルギー差は,
である.これをゼーマン準位と呼ぶ.隣り合う準位間のエネルギー差は,
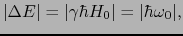 |
|
|
(9.33) |
となっている.これはラーモア周波数に等しい振動数のフォトン(電磁波)のエネルギーが,ちょうどゼーマン準位間のエネルギー差に等しいことを示す.そこで,このようなフォトンはレベル間の遷移を引き起こし吸収されると考えられる.これが磁気共鳴吸収の基本原理である.電子スピン共鳴(Electron Spin Resonance;略してESR)は,フォトンエネルギーとしてマイクロ波を入射し,その一部が電子系に吸収される現象である [ref9].
今回の実験ではマイクロ波の周波数を一定とし,(9.2)式を満たす磁場付近で磁場を掃引してESRを観測する.さらに小さな磁場変調をかけて,雑音に隠れている信号を拾い出すためにロックインアンプを使用する.このとき微分吸収曲線が得られる.マイクロ波の周波数は10 [GHz]程度であるから,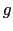 を2程度の大きさとすると,10
を2程度の大きさとすると,10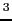 [G]程度の磁場で共鳴吸収が起こることになる.
[G]程度の磁場で共鳴吸収が起こることになる.
マイクロ波の吸収強度を磁場の関数として見たとき,その吸収曲線は多くの場合,(C.19),(C.22)式に基づいて次のようなローレンツ型曲線になる.
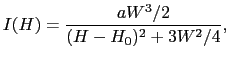 |
|
|
(9.34) |
ここで,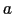 は微分吸収曲線の高さ,
は微分吸収曲線の高さ,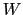 は線幅(微分吸収曲線の極大,極小をとる磁場の幅),
は線幅(微分吸収曲線の極大,極小をとる磁場の幅),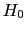 は共鳴磁場を表す.積分強度は
は共鳴磁場を表す.積分強度は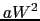 に比例する.
に比例する.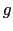 の値は,一般には自由電子のそれとは異なり2.0023からずれることが多い3.
の値は,一般には自由電子のそれとは異なり2.0023からずれることが多い3.
Masashige Onoda
平成18年4月7日
![]() を2程度の大きさとすると,10
を2程度の大きさとすると,10![]() [G]程度の磁場で共鳴吸収が起こることになる.
[G]程度の磁場で共鳴吸収が起こることになる.