


: 常磁性,強磁性の分子場理論とキュリーワイスの法則
: 常磁性・強磁性理論
: 常磁性・強磁性理論
目次
主量子数と方位量子数とで指定される一つ一つの殻を構成する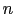 個の電子の
個の電子の
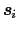 ,
,
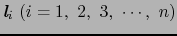 の間には,(a) スピン相互作用,(b) 軌道相互作用,(c) スピン軌道相互作用が存在する.前者二つは,電子間のクーロン力とパウリ原理により生じる.(c)の相互作用は
の間には,(a) スピン相互作用,(b) 軌道相互作用,(c) スピン軌道相互作用が存在する.前者二つは,電子間のクーロン力とパウリ原理により生じる.(c)の相互作用は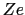 の電荷を持つ原子核のまわりを運動している電子に固定した座標系においてビオ・サバールの法則を考慮に入れれば想像されるだろう.
の電荷を持つ原子核のまわりを運動している電子に固定した座標系においてビオ・サバールの法則を考慮に入れれば想像されるだろう.
ここでは(a),(b)の相互作用が(c)より大きい場合を考える.これを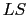 結合の条件という.このときは,(a),(b)の相互作用により原子の最外殻電子のスピン,軌道角運動量がそれぞれ合成されて
結合の条件という.このときは,(a),(b)の相互作用により原子の最外殻電子のスピン,軌道角運動量がそれぞれ合成されて
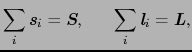 |
|
|
(B..35) |
という原子としての全スピン角運動量,全軌道角運動量をつくる.この
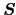 ,
,
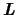 のとり得る値とエネルギーとの関係を記述するものとして,次のフントの規則がある.
のとり得る値とエネルギーとの関係を記述するものとして,次のフントの規則がある.
「パウリの排他律とクーロン相互作用から,スピンは互いに平行になろうとして最大の合成スピン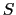 を作る.このときのスピン配列では,合成された軌道角運動量Lの大きさを最大にする軌道配置が最も安定である.」
を作る.このときのスピン配列では,合成された軌道角運動量Lの大きさを最大にする軌道配置が最も安定である.」
(c)のスピン軌道相互作用は,合成された
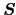 と
と
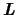 の間の相互作用とみなされる.これは
の間の相互作用とみなされる.これは
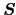 ,
,
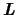 のきまっている準位では,スピン軌道相互作用定数を
のきまっている準位では,スピン軌道相互作用定数を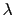 とおくと
とおくと
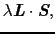 |
|
|
(B..36) |
と書ける.この相互作用を考えれば,
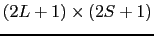 重に縮退した準位は,
重に縮退した準位は,
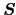 と
と
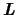 のなす角度によって,エネルギーの異なる準位に分裂する.これを指定するには,図18に示すように,
のなす角度によって,エネルギーの異なる準位に分裂する.これを指定するには,図18に示すように,
図:
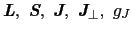 の定義
の定義
|
|
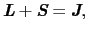 |
|
|
(B..37) |
という全角運動量
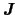 の固有値を用いるとよい.ハイゼンベルグ表示を用いると,
の固有値を用いるとよい.ハイゼンベルグ表示を用いると,
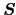 ,
,
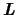 の時間的変化は,
の時間的変化は,
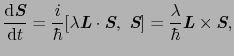 |
|
|
(B..38) |
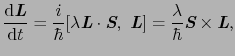 |
|
|
(B..39) |
に従うので,
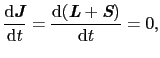 |
|
|
(B..40) |
となり,
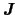 は運動の恒量であることがわかる.古典的にいえば,
は運動の恒量であることがわかる.古典的にいえば,
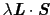 は二つの角運動量
は二つの角運動量
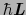 ,
,
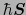 を互いに平行または反平行にさせようとするトルクを生むものだから,
を互いに平行または反平行にさせようとするトルクを生むものだから,
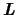 ,
,
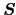 を合わせた系でみれば内力であり,全角運動量
を合わせた系でみれば内力であり,全角運動量
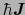 は保存することになる.また,(B.4),(B.5)式は,
は保存することになる.また,(B.4),(B.5)式は,
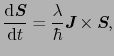 |
|
|
(B..41) |
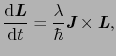 |
|
|
(B..42) |
とも書くことができる.
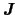 の方向を
の方向を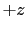 方向とし,その大きさを
方向とし,その大きさを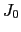 とすると,たとえば,
とすると,たとえば,
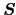 に関しては,
に関しては,
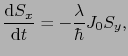 |
|
|
(B..43) |
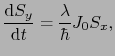 |
|
|
(B..44) |
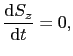 |
|
|
(B..45) |
となるので,(B.11)式から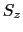 が一定であることがわかる.また,(B.9),(B.10)式から,
が一定であることがわかる.また,(B.9),(B.10)式から,
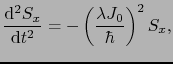 |
|
|
(B..46) |
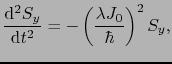 |
|
|
(B..47) |
を得る.これらの解は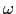 =
=
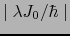 を角周波数とする単振動である.すなわち,
を角周波数とする単振動である.すなわち,
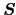 は
は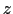 軸と一定の傾きを保ちながら,そのまわりに角周波数
軸と一定の傾きを保ちながら,そのまわりに角周波数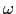 の等速回転運動をすることを意味する.このような運動を歳差運動5という.
の等速回転運動をすることを意味する.このような運動を歳差運動5という.
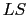 結合では原子の磁気モーメントは,
結合では原子の磁気モーメントは,
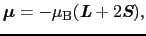 |
|
|
(B..48) |
で与えられる.上で見たように,
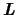 と
と
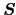 は
は
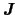 のまわりで歳差運動しているから,
のまわりで歳差運動しているから,
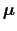 も
も
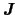 のまわりをまわっている.これを,図18のように,
のまわりをまわっている.これを,図18のように,
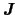 に平行な時間変化のない部分
に平行な時間変化のない部分
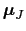 と,
と,
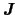 に垂直な時間変化する部分
に垂直な時間変化する部分
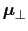 に分けてみよう.すなわち,
に分けてみよう.すなわち,
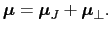 |
|
|
(B..49) |
さらに,
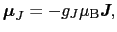 |
|
|
(B..50) |
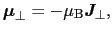 |
|
|
(B..51) |
とおく.(B.16)式の両辺と
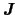 とのスカラー積をつくれば,
とのスカラー積をつくれば,
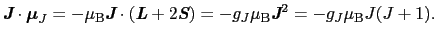 |
|
|
(B..52) |
また,
となる.以上より,(B.16)式の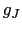 は,
は,
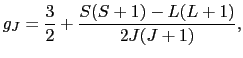 |
|
|
(B..54) |
となる.これをランデの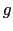 因子という.こうして,内部量子数が
因子という.こうして,内部量子数が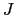 である状態での
である状態での
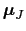 を(B.16),(B.20)式から導くことができる.
を(B.16),(B.20)式から導くことができる.
磁場との相互作用は,
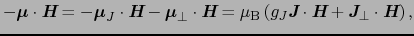 |
|
|
(B..55) |
となる.ここで右辺の第2項6を無視すると,
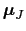 は磁場
は磁場
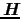 のまわりに歳差運動を行っている.量子論では
のまわりに歳差運動を行っている.量子論では
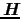 (方向を
(方向を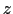 軸にとる)と
軸にとる)と
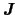 とのなす角度
とのなす角度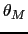 は,
は,
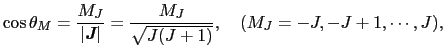 |
|
|
(B..56) |
である7から,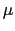
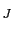 の
の
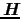 方向への成分の熱平衡状態での平均値は,
方向への成分の熱平衡状態での平均値は,
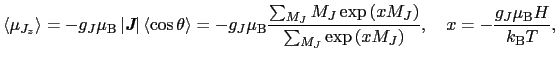 |
|
|
(B..57) |
で与えられる.これは次のように書き換えられる.
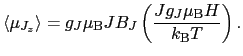 |
|
|
(B..58) |
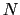 個の原子からなる系の磁化は,
個の原子からなる系の磁化は,
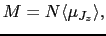 |
|
|
(B..59) |
で与えられる.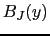 はブリィユアン関数と呼ばれ,次のように定義される.
はブリィユアン関数と呼ばれ,次のように定義される.
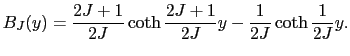 |
|
|
(B..60) |
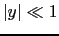 では,
では,
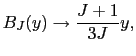 |
|
|
(B..61) |
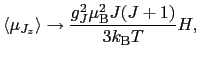 |
|
|
(B..62) |
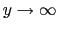 では,
では,
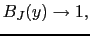 |
|
|
(B..63) |
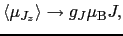 |
|
|
(B..64) |
という性質を持つ.すなわち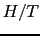 の小さいところでは磁化は磁場に比例するが,
の小さいところでは磁化は磁場に比例するが,
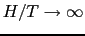 では磁場の強さに依存しなくなり飽和値,
では磁場の強さに依存しなくなり飽和値,
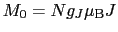 |
|
|
(B..65) |
に達する.この様子を図19に示す.Aはクロムカリ明ばん中のCr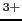 イオン,Bは鉄アンモニア明ばん中のFe
イオン,Bは鉄アンモニア明ばん中のFe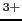 イオン,Cは硫化ガドリニウム8水和物中のGd
イオン,Cは硫化ガドリニウム8水和物中のGd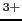 イオンの実験結果である.図中の実線は,(B.24)式でそれぞれ
イオンの実験結果である.図中の実線は,(B.24)式でそれぞれ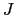 =
= 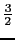 ,
,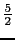 ,
,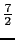 としたときの計算結果である.
としたときの計算結果である.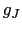 は2とした.
は2とした.
図 19:
実験値[ref6]とブリィユアン関数との比較.Aはクロムカリ明ばん中のCr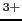 イオン,Bは鉄アンモニウム明ばん中のFe
イオン,Bは鉄アンモニウム明ばん中のFe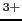 イオン,Cは硫化ガドリニウム8水和物中のGd
イオン,Cは硫化ガドリニウム8水和物中のGd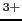 イオンに関する実験結果である.図中の実線は,(B.24)式でそれぞれ
イオンに関する実験結果である.図中の実線は,(B.24)式でそれぞれ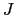 =
= 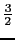 ,
,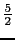 ,
,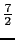 としたときの計算結果で,
としたときの計算結果で,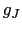 は2とした.
は2とした.
|
|
磁化が磁場に比例する領域での帯磁率は,
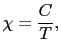 |
|
|
(B..66) |
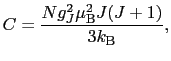 |
|
|
(B..67) |
で与えられる.これをキュリーの法則といい,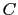 をキュリー定数という.ここでは磁気モーメント間の相互作用は考慮されていないことに注意しよう.
をキュリー定数という.ここでは磁気モーメント間の相互作用は考慮されていないことに注意しよう.



: 常磁性,強磁性の分子場理論とキュリーワイスの法則
: 常磁性・強磁性理論
: 常磁性・強磁性理論
目次
Masashige Onoda
平成18年4月7日
![]() 結合の条件という.このときは,(a),(b)の相互作用により原子の最外殻電子のスピン,軌道角運動量がそれぞれ合成されて
結合の条件という.このときは,(a),(b)の相互作用により原子の最外殻電子のスピン,軌道角運動量がそれぞれ合成されて
![]() を作る.このときのスピン配列では,合成された軌道角運動量Lの大きさを最大にする軌道配置が最も安定である.」
を作る.このときのスピン配列では,合成された軌道角運動量Lの大きさを最大にする軌道配置が最も安定である.」
![]() と
と
![]() の間の相互作用とみなされる.これは
の間の相互作用とみなされる.これは
![]() ,
,
![]() のきまっている準位では,スピン軌道相互作用定数を
のきまっている準位では,スピン軌道相互作用定数を![]() とおくと
とおくと
![]() 結合では原子の磁気モーメントは,
結合では原子の磁気モーメントは,
![\includegraphics[width=8cm, clip]{figure8.eps}](img301.png)