磁気モーメント

図 2.1: 電子の軌道およびスピン磁気モーメント

r0.35

ここではミクロな見地から，物質の磁性について考えてみよう．「電流によって作ることのできないような特殊な磁場はまったく存在しない」というアンペール（Amp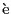$\grave{\rm e}$re）の仮説によれば，物質の磁気的性質は，物質分子あるいは原子内の特殊な電流に起因するはずである．この仮説は，当時（1823年）原子構造についての知識が十分でなかったために，確固とした根拠をもつことができなかった．どんな原子でも，原子核を中心にしてその周囲をいくつかの電子が回っていることがわかってはじめて，磁性の基本的な担い手である電流が電子によるものであることが明らかになったのである．

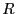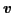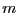太陽の周りを，地球が自転しながら公転しているように，電子も自転しながら原子核の周囲の半径$R$の電子軌道を公転しているモデルを考えよう（図2.1）．電子の速度を $\mbox{\bfseries\itshape {v}}$，質量を$m$とすれば，円運動しているときの角運動量 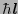$\hbar\mbox{\bfseries\itshape {l}}$は^2.1，

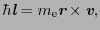$$\hbar\mbox{\bfseries\itshape {l}} = m_{\rm e}\mbox{\bfseries\itshape {r}} \times \mbox{\bfseries\itshape {v}},$$ (2.1.1)

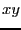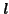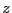で与えられる．この円軌道が直交座標系の$xy$面内にあり， $\mbox{\bfseries\itshape {l}}$は$z$成分以外はゼロであるとすれば，

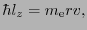$$\hbar l_{z} = m_{\rm e}rv,$$ (2.1.2)

である．電子は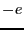$-e$の電荷をもっているので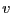，$v$の速さの円運動は，

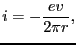$$i = - {ev \over{2\pi r}},$$ (2.1.3)

の電流に相当する．この円電流が一様な磁場の中にあるときに受ける力のモーメントを 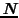$\mbox{\bfseries\itshape {N}}$とおくとき，

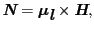$$\mbox{\bfseries\itshape {N}} = \mbox{\boldmath$\mu$}_{\mbox{\bfseries\itshape {l}}} \times \mbox{\bfseries\itshape {H}},$$ (2.1.4)

で定義される軌道磁気モーメント 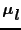$\mbox{\boldmath$\mu$}_{\mbox{\bfseries\itshape {l}}}$の大きさは，

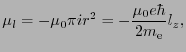$$\mu_{l} = -\mu_{0}\pi ir^{2} = - {\mu_{0}e\hbar \over{2m_{\rm e}}}l_{z},$$ (2.1.5)

である^2.2．これをベクトルで表せば，

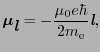$$\mbox{\boldmath$\mu$}_{\mbox{\bfseries\itshape {l}}} = - {\mu_{0}e\hbar \over{2m_{\rm e}}}\mbox{\bfseries\itshape {l}},$$ (2.1.6)

となる．しかし，電子や原子の性質を詳しく論じるためにはこのような古典力学では不正確であって，量子力学によらねばならない．今，

$$\mu_{\rm B} = {\mu_{0}e\hbar \over{2m_{\rm e}}}\ [{\rm Wbm}],$$ (2.1.7)

または，

$$\mu_{\rm B} = {e\hbar \over{2m_{\rm e}}}\ [{\rm JT^{-1}}],$$ (2.1.8)

で定義されるボーア磁子を使えば，軌道磁気モーメントは，

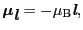$$\mbox{\boldmath$\mu$}_{\mbox{\bfseries\itshape {l}}} = - \mu_{\rm B}\mbox{\bfseries\itshape {l}},$$ (2.1.9)

と書ける．

さらに，電子の自転も磁石の性質をもつ．これにより生じる磁気モーメントをスピン磁気モーメントという．電子スピンという概念を完全に理解するためには，量子力学，特に相対論的量子力学に立ち入る必要があり，ここでは詳しい議論は省略する^2.3．スピン数を 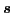$\mbox{\bfseries\itshape {s}}$とすれば，その磁気モーメントは，

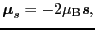$$\mbox{\boldmath$\mu$}_{s} = - 2\mu_{\rm B}\mbox{\bfseries\itshape {s}},$$ (2.1.10)

である．原子の磁気モーメントはこれらのモーメントの和^2.4，

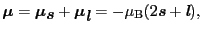$$\mbox{\boldmath$\mu$} = \mbox{\boldmath$\mu$}_{\mbox{\bfseries\it... ... = - \mu_{\rm B}(2\mbox{\bfseries\itshape {s}} + \mbox{\bfseries\itshape {l}}),$$ (2.1.11)

で与えられる．

これまで述べたことは孤立した原子に対しての話であることに注意してほしい．アボガドロ数程度の原子からなる固体の磁気モーメントには，各原子から生じる部分だけでなく，隣接原子の相互作用によって生じる部分もある．