- ...小野田 雅 重1
- e-mail: onoda@sakura.cc.tsukuba.ac.jp
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...は2.1
- 物理学A I参照
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
である2.2
- 微小な円形電流
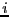 のつくる磁場と,正負の磁荷というものが存在すると仮定したときの磁石のつくる磁場と比較することにより,円形電流と磁石とが,それらのまわりの空間につくる磁場に関して等価であることが示される.まず,
のつくる磁場と,正負の磁荷というものが存在すると仮定したときの磁石のつくる磁場と比較することにより,円形電流と磁石とが,それらのまわりの空間につくる磁場に関して等価であることが示される.まず,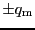 の磁荷を距離
の磁荷を距離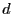 だけ離しておくことによりつくられる磁気モーメント
だけ離しておくことによりつくられる磁気モーメント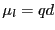 が,モーメントの向きに沿って
が,モーメントの向きに沿って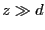 の場所につくる磁場の強さを計算する.次に,半径
の場所につくる磁場の強さを計算する.次に,半径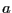 の円形電流がその中心軸上の
の円形電流がその中心軸上の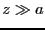 の場所につくる磁場の強さを求める.これらを比較することにより,
の場所につくる磁場の強さを求める.これらを比較することにより,
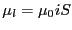 の関係が得られる.
の関係が得られる.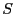 は円形電流の面積である.
は円形電流の面積である.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...スピン磁気モーメントという.電子スピンという概念を完全に理解するためには,量子力学,特に相対論的量子力学に立ち入る必要があり,ここでは詳しい議論は省略する2.3
- 1925年にウーレンベック(Uhlenbeck)とハウトスミット(Goudsmit)によって提唱された.スピンの概念は,後にディラック(Dirac)の理論により無理なく導き出されたが,そもそものはじまりはそれまで説明できなかった実験事実の解釈の必要から提出された.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
である.原子の磁気モーメントはこれらのモーメントの和2.4
- 陽子と中性子の磁気モーメントは,電子のものに比べて小さいことが知られており,原子の磁気的性質は,主として電子殻の性質によって決まると考えて差し支えない.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
ここで磁化測定の方法について紹介しておこう2.5
- 物理学実験 III--磁気測定--参照
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... [T]程度の超伝導磁石による浮上現象が1991年に報告された.その後,生物に対する磁場効果2.6
- 第4章を参照のこと
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...の観点から水への磁場効果に興味が持たれ,いわゆるモーゼ効果が確かめられた.モーゼ効果とは,水平型磁石の中で水槽中の水面が割れたり,硫酸銅水溶液の液面が盛り上がったりする様をたとえている2.7
- 映画「十戒」では,逃げ場を失った追われる民が,モーゼの神通力で海面の割れた海を渡って大脱出する光景が登場する.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...強磁性が電子の軌道磁気モーメントだけに起因すると仮定すれば,強く磁化した鉄片では,これらのモーメントはすべて一方向を向いているであろう.すなわち,各電子の軌道面は互いに平行で,電子はすべて同じ向きに回転しなければならない.すなわち鉄片の中には,多数の小さな車輪があって,これが一定方向に回転していると考えてよい.今,この鉄片の磁化を逆転したとすれば,電子は今までと逆の方向へ回転し始める.これにより,鉄片は,角運動量保存則2.8
- 物理学A I参照
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...を例に2.9
- M. Onoda and N. Nishiguchi, J. Phys.: Condens. Matter (1999)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...歳差運動2.10
- 歳差運動の他の例としては,重力場におけるこまの回転運動が知られている.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
となる.ここで右辺の第2項2.11
- この効果を分極効果という.量子論的にいえば,摂動項
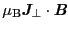 によって,磁場のないときの基底状態の(2
によって,磁場のないときの基底状態の(2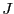 + 1)重に縮退した波動関数に,励起状態が混ざってくることである.一方,
+ 1)重に縮退した波動関数に,励起状態が混ざってくることである.一方,
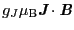 の効果を配向効果と呼ぶことがある.
の効果を配向効果と呼ぶことがある.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
である2.12
- 量子力学的な固有状態で
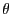 がはっきり一定値をとるわけではなく,
がはっきり一定値をとるわけではなく,
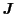 の成分
の成分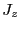 の期待値が
の期待値が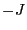 から
から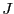 までの
までの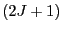 個の値のいずれかをとる.
個の値のいずれかをとる.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...交換相互作用2.13
- 交換相互作用が水素分子の結合エネルギーに本質的役割を演じることは,ハイトラーロンドンの理論として知られている.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...は種々の波動関数に対する平均とする2.14
- (2.6.41)式の形の相互作用はハイゼンベルグの考えたような直接交換相互作用だけでなく,もっと複雑な機構によっても現れる.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...が小さくても有限の物質では,十分温度を下げれば常磁性状態はたいてい強磁性をはじめとするスピンの秩序状態に移行する.実際の強磁性体では外部磁場をかけないときは磁化は0であるが,非常に小さい磁場で容易に飽和値まで磁化される.これは,強磁性体内では自発磁化をもっている小区域が多数あって,外部磁場のないときには小区域ごとに自発磁化の方向が異なっており,全体としてみれば各小区域の磁化が打ち消し合っているためである2.15
- 磁場0でも試料全体で準安定的にスピンが一様に揃って磁化をもっている物質が永久磁石である.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...バナジウム酸化物2.16
- 高温超伝導酸化物の超伝導発現機構や種々の低次元スピンネットワークを持つ
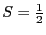 系の構造・物性の解明は,物性物理学研究における最重要課題の一つである.
系の構造・物性の解明は,物性物理学研究における最重要課題の一つである.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...eqn:5420)式にほぼ従う2.17
- 図2.7(a)および図2.7(b)の実線は,より進んだモデルに基づく計算結果である.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
近年に進歩した画像診断の代表にCT4.1
- 付録A参照
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Imaging)の略であり,核磁気共鳴という物理学の原理を利用して,内臓の三次元画像や断層画像を撮影する検査法をいう4.2
- 以前は,NMRと断層撮影装置(Computer Tomography)の略語であるCTを合わせてNMRCTと呼ばれていたが,最近はMRIと呼ばれるようになった.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.