


: スピンの運動,磁気共鳴
: 理論の本質
: 原子の常磁性
目次
前にも述べたように強磁性を示す物質では,それを構成している原子またはイオンが不完全殻から生じる磁気モーメントをもち,それらが全て一方向に揃っている.強磁性に関係する磁気モーメントは一般には電子スピンからの寄与であるので,この節では電子スピン間の相互作用と磁気的性質との関係について説明する.
電子スピン間の相互作用として最初に考えられるのは電子スピン間の磁気相互作用である.この大きさは磁気モーメントの積と距離の3乗の逆数との積
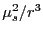 で近似的に与えられる.今,
で近似的に与えられる.今,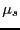 としてボーア磁子〜
としてボーア磁子〜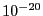 [erg G
[erg G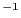 ],
],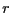 として原子間距離〜
として原子間距離〜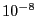 [cm]をとると,それは
[cm]をとると,それは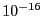 [erg]で,温度に換算して約1 [K]となる.このように弱い相互作用ではとても強磁性の原因とは考えられない.
[erg]で,温度に換算して約1 [K]となる.このように弱い相互作用ではとても強磁性の原因とは考えられない.
強磁性体の電子スピン間の相互作用が量子効果として現れる交換相互作用2.13であることを示したのはハイゼンベルグである.軌道波動関数が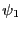 と
と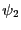 であるような二つの状態に入っている二つの電子の間には,次の交換相互作用が働く.
であるような二つの状態に入っている二つの電子の間には,次の交換相互作用が働く.
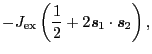 |
|
|
(2.6.60) |
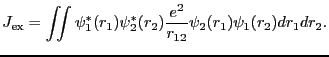 |
|
|
(2.6.61) |
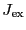 は交換相互作用定数と呼ばれる.この大きさは,クーロン積分と同程度の大きさを持つ.(2.6.39)式は多電子系の中の2電子についても成立する.
は交換相互作用定数と呼ばれる.この大きさは,クーロン積分と同程度の大きさを持つ.(2.6.39)式は多電子系の中の2電子についても成立する.
いま固体を構成している各原子において等しい整数個の電子がフントの規則に従って最大のスピンを形成して,隣合う原子間に交換相互作用が働くとする.このとき(2.6.39)式における
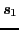 ,
,
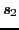 は第1,2原子の全スピン
は第1,2原子の全スピン
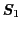 ,
,
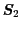 で置き換えられる.最終的な原子間交換相互作用の表式は定数項を除いて,
で置き換えられる.最終的な原子間交換相互作用の表式は定数項を除いて,
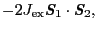 |
|
|
(2.6.62) |
となる.ただし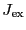 は種々の波動関数に対する平均とする2.14.
は種々の波動関数に対する平均とする2.14.
一般にこの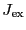 の大きさと温度に依存しながら,物質は強磁性を示したり常磁性を示したりする.常磁性体では各原子の磁気モーメント間の相互作用が小さくて,各磁気モーメントは熱運動のためにでたらめの方向を向いているが磁場をかけると磁気モーメントが磁場の方向に部分的に揃い全体として磁化されるのに対して,強磁性体ではこの相互作用が強くて磁場が0でも互いに規則正しい配列をしている.このときの強磁性体の磁化を自発磁化と呼ぶ.特にFe,Co,Niなどは
の大きさと温度に依存しながら,物質は強磁性を示したり常磁性を示したりする.常磁性体では各原子の磁気モーメント間の相互作用が小さくて,各磁気モーメントは熱運動のためにでたらめの方向を向いているが磁場をかけると磁気モーメントが磁場の方向に部分的に揃い全体として磁化されるのに対して,強磁性体ではこの相互作用が強くて磁場が0でも互いに規則正しい配列をしている.このときの強磁性体の磁化を自発磁化と呼ぶ.特にFe,Co,Niなどは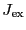 が非常に大きく,常温でもスピンがほとんど揃っている.しかし温度が十分に高くなって熱運動がこの相互作用を凌ぐようになれば,常磁性を示すようになることが期待される.言い換えれば
が非常に大きく,常温でもスピンがほとんど揃っている.しかし温度が十分に高くなって熱運動がこの相互作用を凌ぐようになれば,常磁性を示すようになることが期待される.言い換えれば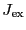 が小さくても有限の物質では,十分温度を下げれば常磁性状態はたいてい強磁性をはじめとするスピンの秩序状態に移行する.実際の強磁性体では外部磁場をかけないときは磁化は0であるが,非常に小さい磁場で容易に飽和値まで磁化される.これは,強磁性体内では自発磁化をもっている小区域が多数あって,外部磁場のないときには小区域ごとに自発磁化の方向が異なっており,全体としてみれば各小区域の磁化が打ち消し合っているためである2.15.以下の理論は,この一つの小区域に対して適用される.
が小さくても有限の物質では,十分温度を下げれば常磁性状態はたいてい強磁性をはじめとするスピンの秩序状態に移行する.実際の強磁性体では外部磁場をかけないときは磁化は0であるが,非常に小さい磁場で容易に飽和値まで磁化される.これは,強磁性体内では自発磁化をもっている小区域が多数あって,外部磁場のないときには小区域ごとに自発磁化の方向が異なっており,全体としてみれば各小区域の磁化が打ち消し合っているためである2.15.以下の理論は,この一つの小区域に対して適用される.
各原子に番号を付けて,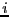 原子の隣の
原子の隣の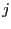 原子を考え,全系の交換エネルギーを,
原子を考え,全系の交換エネルギーを,
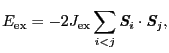 |
|
|
(2.6.63) |
と書く.この式の固有値を求めて熱平衡における状態和を計算するのは難しいので,ここでは
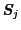 を
を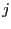 に依存しない熱平均値
に依存しない熱平均値
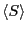 で近似する.(2.6.42)式の中から一つの
で近似する.(2.6.42)式の中から一つの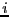 とそのまわりの最近接相互作用を取り出すと,
とそのまわりの最近接相互作用を取り出すと,
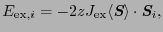 |
|
|
(2.6.64) |
となる.ここで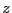 は最近接対の数を表す.(2.6.43)式を,
は最近接対の数を表す.(2.6.43)式を,
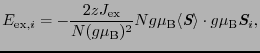 |
|
|
(2.6.65) |
とおくと,
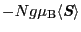 は全系の磁気モーメントに,
は全系の磁気モーメントに,
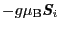 は
は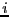 原子の磁気モーメントに対応する.または,
原子の磁気モーメントに対応する.または,
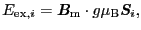 |
|
|
(2.6.66) |
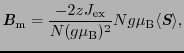 |
|
|
(2.6.67) |
と書き換えることもできる.
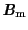 を分子場と呼び,この種の近似で展開される理論を分子場理論と呼ぶ.
を分子場と呼び,この種の近似で展開される理論を分子場理論と呼ぶ.
上記の理論に従って,最初に強磁性体の自発磁化の温度依存性を求めてみよう.
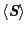 に関しては,(2.6.29)式で
に関しては,(2.6.29)式で
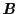 の代わりに
の代わりに
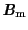 をとり,
をとり,
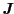 の代わりに
の代わりに
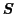 をとればよい.
をとればよい.
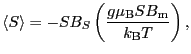 |
|
|
(2.6.68) |
この式の解は,両辺を
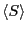 の関数として図を描き,その交点を求めることによって得られる.図2.11からわかるように,もし右辺の関数の0付近の傾きが45
の関数として図を描き,その交点を求めることによって得られる.図2.11からわかるように,もし右辺の関数の0付近の傾きが45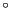 よりも小さいときには
よりも小さいときには
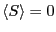 の解しか存在しない.これは磁場0では磁気モーメントがでたらめな方向を向いていることに相当する.一方傾きが45
の解しか存在しない.これは磁場0では磁気モーメントがでたらめな方向を向いていることに相当する.一方傾きが45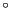 よりも大きいときは
よりも大きいときは
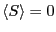 の他に
の他に
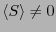 の解も存在する.両者の自由エネルギーの大小関係から,実際には
の解も存在する.両者の自由エネルギーの大小関係から,実際には
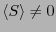 の状態が実現し,これは磁気モーメントが揃ってきている状態に相当する.ここで傾きが45
の状態が実現し,これは磁気モーメントが揃ってきている状態に相当する.ここで傾きが45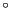 になる温度は,
になる温度は,
 |
|
|
(2.6.69) |
で与えられる.この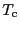 を強磁性体ではキュリー温度と呼ぶ.
を強磁性体ではキュリー温度と呼ぶ.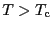 では
では
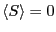 の常磁性状態であるが,
の常磁性状態であるが,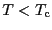 では
では
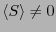 の強磁性状態が実現しており,自発磁化が生じる.
の強磁性状態が実現しており,自発磁化が生じる.
この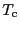 を用いると(2.6.47)式は,
を用いると(2.6.47)式は,
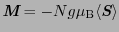 |
|
|
(2.6.70) |
の関係から,
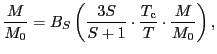 |
|
|
(2.6.71) |
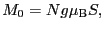 |
|
|
(2.6.72) |
に書き換えられる.ここで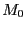 は
は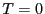 での磁化に対応する.
での磁化に対応する.
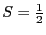 のときの
のときの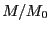 と
と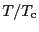 との関係を図2.12に示す.
との関係を図2.12に示す.
図:
ニッケル金属の実験値と
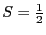 のときの(2.6.47)式の計算曲線との比較
のときの(2.6.47)式の計算曲線との比較
|
|
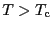 では外部磁場
では外部磁場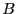 が働いてはじめて磁化される.外部磁場が働いたときはスピン間の相互作用による分子場
が働いてはじめて磁化される.外部磁場が働いたときはスピン間の相互作用による分子場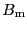 が生じるから,
が生じるから,
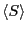 は,
は,
![$\displaystyle \langle S \rangle
=
- SB_{S} \left [ \frac{g\mu_{\rm B}S ( B_{\rm m} + B )}{k_{\rm B}T} \right ],$](img253.png) |
|
|
(2.6.73) |
となる.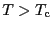 では
では
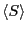 は
は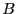 に比例するから,
に比例するから,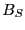 で
で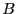 に比例する項のみ残すと,
に比例する項のみ残すと,
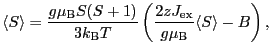 |
|
|
(2.6.74) |
あるいは,
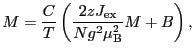 |
|
|
(2.6.75) |
が得られる.ここで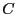 は(2.6.38)式のキュリー定数で,
は(2.6.38)式のキュリー定数で,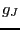 ,
,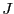 はそれぞれ
はそれぞれ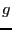 ,
,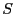 に置き換えられている.これから帯磁率は,
に置き換えられている.これから帯磁率は,
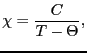 |
|
|
(2.6.76) |
となる.この関係式をキュリーワイスの法則と呼ぶ.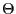 は(2.6.48)式のキュリー温度
は(2.6.48)式のキュリー温度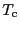 に等しい.帯磁率の逆数
に等しい.帯磁率の逆数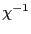 は温度に関して直線で温度軸を
は温度に関して直線で温度軸を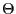 で切る.図2.7にV
で切る.図2.7にV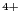 の孤立ジグザグ鎖をもつCdVO
の孤立ジグザグ鎖をもつCdVO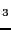 の磁気的性質を示す.本物質は,3d
の磁気的性質を示す.本物質は,3d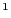 バナジウム酸化物2.16では珍しい,キュリー温度
バナジウム酸化物2.16では珍しい,キュリー温度
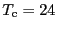 [K],
[K],
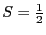 の強磁性体である.帯磁率は,約120 [K]以上において,図2.7(a)中の破線のように,(2.6.55)式のキュリーワイスの法則で説明され,また自発磁化の温度依存性は,図2.7(c)中の実線で示されるように,(2.6.47)式にほぼ従う2.17.ここで,
の強磁性体である.帯磁率は,約120 [K]以上において,図2.7(a)中の破線のように,(2.6.55)式のキュリーワイスの法則で説明され,また自発磁化の温度依存性は,図2.7(c)中の実線で示されるように,(2.6.47)式にほぼ従う2.17.ここで,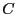 および
および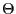 は,それぞれ0.371 [emu K mol
は,それぞれ0.371 [emu K mol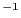 ]および39.2 [K]である.
]および39.2 [K]である.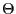 の値が
の値が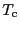 と大きく異なっているが,これはさらに分子場理論の精度を高めることによって説明することができる.
温度が
と大きく異なっているが,これはさらに分子場理論の精度を高めることによって説明することができる.
温度が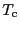 の近傍では,磁化曲線に対する自発磁化の寄与と常磁性の寄与が区別しにくくなる.この場合
の近傍では,磁化曲線に対する自発磁化の寄与と常磁性の寄与が区別しにくくなる.この場合
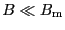 を考慮すると,(2.6.52)式は,
を考慮すると,(2.6.52)式は,
![$\displaystyle \langle S \rangle^{2}
=
\frac{10T^{2}S^{2}(S+1)^{2}}{3\Theta^{3}[...
... + \frac{g\mu_{\rm B}\Theta}{2zJ_{\rm ex}}\frac{B}{\langle S \rangle} \right ],$](img264.png) |
|
|
(2.6.77) |
あるいは,
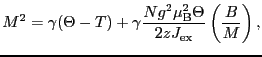 |
|
|
(2.6.78) |
![$\displaystyle \gamma
=
\frac{10T^{2}M_{0}^{2}(S + 1)^{2}}{3\Theta^{3}[(S + 1)^{2} + S^{2}]},$](img266.png) |
|
|
(2.6.79) |
と近似される.したがって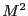 を
を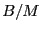 に対してプロットすれば,その切片から自発磁化は次のように評価される.
に対してプロットすれば,その切片から自発磁化は次のように評価される.
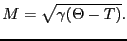 |
|
|
(2.6.80) |



: スピンの運動,磁気共鳴
: 理論の本質
: 原子の常磁性
目次
Masashige Onoda
平成18年4月11日
![]() で近似的に与えられる.今,
で近似的に与えられる.今,![]() としてボーア磁子〜
としてボーア磁子〜![]() [erg G
[erg G![]() ],
],![]() として原子間距離〜
として原子間距離〜![]() [cm]をとると,それは
[cm]をとると,それは![]() [erg]で,温度に換算して約1 [K]となる.このように弱い相互作用ではとても強磁性の原因とは考えられない.
[erg]で,温度に換算して約1 [K]となる.このように弱い相互作用ではとても強磁性の原因とは考えられない.
![]() と
と![]() であるような二つの状態に入っている二つの電子の間には,次の交換相互作用が働く.
であるような二つの状態に入っている二つの電子の間には,次の交換相互作用が働く.
![]() ,
,
![]() は第1,2原子の全スピン
は第1,2原子の全スピン
![]() ,
,
![]() で置き換えられる.最終的な原子間交換相互作用の表式は定数項を除いて,
で置き換えられる.最終的な原子間交換相互作用の表式は定数項を除いて,
![]() の大きさと温度に依存しながら,物質は強磁性を示したり常磁性を示したりする.常磁性体では各原子の磁気モーメント間の相互作用が小さくて,各磁気モーメントは熱運動のためにでたらめの方向を向いているが磁場をかけると磁気モーメントが磁場の方向に部分的に揃い全体として磁化されるのに対して,強磁性体ではこの相互作用が強くて磁場が0でも互いに規則正しい配列をしている.このときの強磁性体の磁化を自発磁化と呼ぶ.特にFe,Co,Niなどは
の大きさと温度に依存しながら,物質は強磁性を示したり常磁性を示したりする.常磁性体では各原子の磁気モーメント間の相互作用が小さくて,各磁気モーメントは熱運動のためにでたらめの方向を向いているが磁場をかけると磁気モーメントが磁場の方向に部分的に揃い全体として磁化されるのに対して,強磁性体ではこの相互作用が強くて磁場が0でも互いに規則正しい配列をしている.このときの強磁性体の磁化を自発磁化と呼ぶ.特にFe,Co,Niなどは![]() が非常に大きく,常温でもスピンがほとんど揃っている.しかし温度が十分に高くなって熱運動がこの相互作用を凌ぐようになれば,常磁性を示すようになることが期待される.言い換えれば
が非常に大きく,常温でもスピンがほとんど揃っている.しかし温度が十分に高くなって熱運動がこの相互作用を凌ぐようになれば,常磁性を示すようになることが期待される.言い換えれば![]() が小さくても有限の物質では,十分温度を下げれば常磁性状態はたいてい強磁性をはじめとするスピンの秩序状態に移行する.実際の強磁性体では外部磁場をかけないときは磁化は0であるが,非常に小さい磁場で容易に飽和値まで磁化される.これは,強磁性体内では自発磁化をもっている小区域が多数あって,外部磁場のないときには小区域ごとに自発磁化の方向が異なっており,全体としてみれば各小区域の磁化が打ち消し合っているためである2.15.以下の理論は,この一つの小区域に対して適用される.
が小さくても有限の物質では,十分温度を下げれば常磁性状態はたいてい強磁性をはじめとするスピンの秩序状態に移行する.実際の強磁性体では外部磁場をかけないときは磁化は0であるが,非常に小さい磁場で容易に飽和値まで磁化される.これは,強磁性体内では自発磁化をもっている小区域が多数あって,外部磁場のないときには小区域ごとに自発磁化の方向が異なっており,全体としてみれば各小区域の磁化が打ち消し合っているためである2.15.以下の理論は,この一つの小区域に対して適用される.
![]() 原子の隣の
原子の隣の![]() 原子を考え,全系の交換エネルギーを,
原子を考え,全系の交換エネルギーを,
![]() を用いると(2.6.47)式は,
を用いると(2.6.47)式は,