



: 有限温度への拡張
: BCS理論
: 励起状態とエネルギーギャップ
目次
この理論はハートリーフォック近似を拡張したものである7.1.これまでの仮定を含めて()式をもう一度書く.
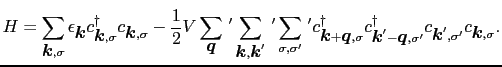 |
|
|
(7.11.107) |
ここで以下の変換を考える.
これらを逆に解くと,
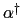 ,
,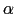 もフェルミの交換関係を満たす.
もフェルミの交換関係を満たす.
![$\displaystyle \ [ \alpha_{\mbox{\boldmath$k$} \sigma}, \alpha_{\mbox{\boldmath$...
...\ ] = \delta_{\mbox{\boldmath$k$} \mbox{\boldmath$k$}'}\delta_{\sigma \sigma'}.$](img1510.png) |
|
|
(7.11.110) |
(7.11.29)式を(7.11.27)式に代入し,
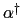 ,
,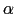 で表す.たとえば,
で表す.たとえば,
などと変形する.相互作用の項の計算は面倒であるが,丁寧に行えばできる.結果はハミルトニアン全体として,
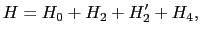 |
|
|
(7.11.111) |
ここで,
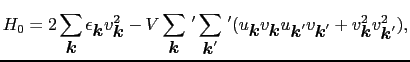 |
|
|
(7.11.112) |
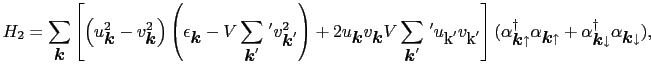 |
|
|
(7.11.113) |
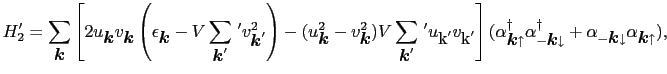 |
|
|
(7.11.114) |
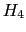 は4次の項であり多くの項を含んでいるが,後に必要になる項だけを書くことにする.
は4次の項であり多くの項を含んでいるが,後に必要になる項だけを書くことにする.
基底状態は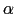 についての真空状態,
についての真空状態,
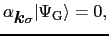 |
|
|
(7.11.116) |
であるとする.エネルギー期待値として残るのは,
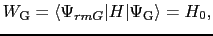 |
|
|
(7.11.117) |
である.この式を最小にする
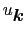 ,
,
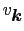 は,変分法により
は,変分法により
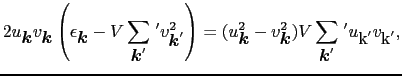 |
|
|
(7.11.118) |
である.(7.11.38)式は,(7.11.34)式の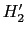 = 0という条件に他ならず,これは,ハートリーフォック近似では2次の項の非対角項がゼロになることを確認したことにすぎない.
= 0という条件に他ならず,これは,ハートリーフォック近似では2次の項の非対角項がゼロになることを確認したことにすぎない.
(7.11.38)式は,(7.11.8),(7.11.9)式と比べれば,
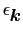 の代わりに
の代わりに
が現れているだけで,あとは同じである.この余分な項はBCSでも小さいものとして無視しており,この方法はBCSと全く同等であることがわかる.これを無視すれば,()式の解は(7.11.10),(7.11.10)式と同じである.
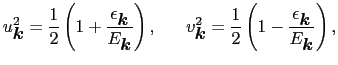 |
|
|
(7.11.119) |
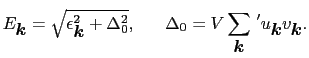 |
|
|
(7.11.120) |
(7.11.39),(7.11.40)式を(7.11.33)式に代入すると,
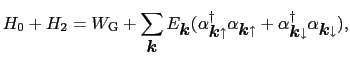 |
|
|
(7.11.121) |
を得る.こうしてBCS理論はハミルトニアン形式で書き直された.種々の物理量は(7.11.29)式のボゴリューボフ変換によって
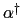 ,
,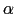 で書き表すことができるので,計算も形式的にできる.
で書き表すことができるので,計算も形式的にできる.




: 有限温度への拡張
: BCS理論
: 励起状態とエネルギーギャップ
目次
Masashige Onoda
平成18年4月7日
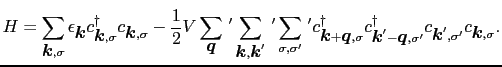
![]() についての真空状態,
についての真空状態,
![]() の代わりに
の代わりに