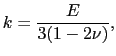: 弾性歪みエネルギー
: 連続体の力学
: 応力とひずみ
歪み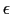 が十分に小さければ,一般に,
が十分に小さければ,一般に,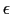 と応力
と応力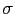 は比例関係,
は比例関係,
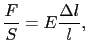 |
|
|
(6.2.4) |
にある.これをフックの法則といい,比例定数 を弾性率と呼ぶ.
を弾性率と呼ぶ.
応力が張力で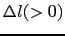 ,歪みが
,歪みが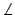 の場合,(6.2.1)式は,
の場合,(6.2.1)式は,
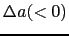 |
|
|
(6.2.5) |
となり,このときの弾性率 を特にヤング率という.
を特にヤング率という.
図6.5のように,弾性体を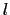 から
から
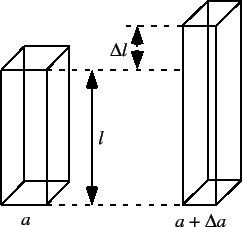 だけ引き伸ばすと,延伸方向に垂直な断面の寸法
だけ引き伸ばすと,延伸方向に垂直な断面の寸法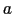 が
が
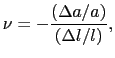 だけ減少することが,経験的に知られている.
だけ減少することが,経験的に知られている.
このとき,
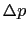 |
|
|
(6.2.6) |
で定義される比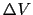 をポアッソン比という.
をポアッソン比という.
地上の物体は,すべて表面に垂直に一様な大気圧を受けている.表面に垂直な圧力が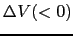 だけ加わると,
だけ加わると,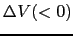 = 0のとき
= 0のとき であった物体の体積は減少する.-
であった物体の体積は減少する.-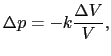 を体積の減少分とすると,
を体積の減少分とすると,
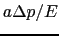 はもとの体積
はもとの体積 にも比例するし,増加した圧力
にも比例するし,増加した圧力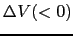 にも比例する.したがって,
にも比例する.したがって,
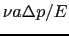 |
|
|
(6.2.7) |
となる.ここで比例定数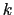 を体積弾性率といい,その逆数1/
を体積弾性率といい,その逆数1/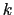 を圧縮率という.
を圧縮率という.
中に境目のない結晶(単結晶という)についてヤング率を測ると,その値は一般に,方向によって異なる.木材なども木材繊維の方向とそれに直角な方向ではヤング率が違う.こういう物質を異方性があるという.これに対して,いろいろな方向をもつ単結晶が集まった結晶(多結晶という)では,異方性が平均化されて方向による違いは現れない.このような性質を等方性という.
実用されている材料の多くは等方性とみなしてよい.等方性物質の場合,ヤング率 ,ポアッソン比
,ポアッソン比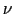 ,体積弾性率
,体積弾性率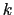 は互いに独立な定数というわけではない.一辺の長さが
は互いに独立な定数というわけではない.一辺の長さが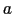 の立方体を考えよう.上下の面だけに外から一様な圧力
の立方体を考えよう.上下の面だけに外から一様な圧力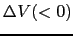 を加えたとすると,立方体は上下方向に
を加えたとすると,立方体は上下方向に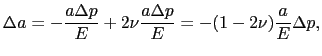 だけ縮み,左右と前後に
だけ縮み,左右と前後に
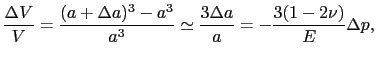 だけ伸びる.歪みがあまり大きくないときは,重ね合せが成り立つので,立方体の上下,左右,前後に圧力
だけ伸びる.歪みがあまり大きくないときは,重ね合せが成り立つので,立方体の上下,左右,前後に圧力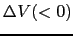 を加えたことによる伸び縮みの合計は,
を加えたことによる伸び縮みの合計は,
となる.したがって,
として,体積変化の割合が表される.これと(6.2.4)式とを比較することにより,
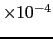 |
|
|
(6.2.8) |
を得る.どんな物体でも圧力を加えれば体積は減る.すなわち必ず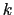
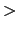 0である.
0である. も必ず正であるから,
も必ず正であるから,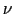
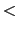 0.5でなければならない.表6.1に主な物質のヤング率,ポアッソン比,体積弾性率を示しておく.
0.5でなければならない.表6.1に主な物質のヤング率,ポアッソン比,体積弾性率を示しておく.
表 6.1:
主な物質のヤング率,ポアッソン比,体積弾性率
| 物 質 |
ヤング率  [10 [10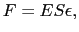 N m N m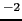 ] ] |
ポアッソン比 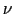 |
体積弾性率 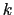 [10 [10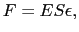 N m N m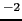 ] ] |
| 鋼 鉄 |
20.1〜21.6 |
0.28〜0.30 |
16.5〜17.0 |
| アルミニウム |
7.03 |
0.345 |
7.55 |
| 金 |
7.8 |
0.44 |
21.7 |
| 銀 |
8.27 |
0.367 |
10.36 |
| 銅 |
12.98 |
0.343 |
13.78 |
| 鉛 |
1.61 |
0.44 |
4.58 |
| ガ ラ ス |
8.01 |
0.27 |
5.76 |
| ゴ ム |
(1.5〜5.0)
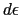 |
0.46〜0.49 |
-- |



: 弾性歪みエネルギー
: 連続体の力学
: 応力とひずみ
Masashige Onoda
平成18年4月15日
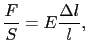
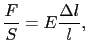
![]() ,歪みが
,歪みが![]() の場合,(6.2.1)式は,
の場合,(6.2.1)式は,
![]() から
から
 だけ引き伸ばすと,延伸方向に垂直な断面の寸法
だけ引き伸ばすと,延伸方向に垂直な断面の寸法![]() が
が
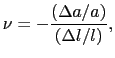 だけ減少することが,経験的に知られている.
だけ減少することが,経験的に知られている.
![]() だけ加わると,
だけ加わると,![]() = 0のとき
= 0のとき![]() であった物体の体積は減少する.-
であった物体の体積は減少する.-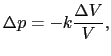 を体積の減少分とすると,
を体積の減少分とすると,
![]() はもとの体積
はもとの体積![]() にも比例するし,増加した圧力
にも比例するし,増加した圧力![]() にも比例する.したがって,
にも比例する.したがって,
![]() ,ポアッソン比
,ポアッソン比![]() ,体積弾性率
,体積弾性率![]() は互いに独立な定数というわけではない.一辺の長さが
は互いに独立な定数というわけではない.一辺の長さが![]() の立方体を考えよう.上下の面だけに外から一様な圧力
の立方体を考えよう.上下の面だけに外から一様な圧力![]() を加えたとすると,立方体は上下方向に
を加えたとすると,立方体は上下方向に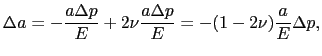 だけ縮み,左右と前後に
だけ縮み,左右と前後に
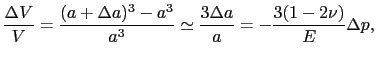 だけ伸びる.歪みがあまり大きくないときは,重ね合せが成り立つので,立方体の上下,左右,前後に圧力
だけ伸びる.歪みがあまり大きくないときは,重ね合せが成り立つので,立方体の上下,左右,前後に圧力![]() を加えたことによる伸び縮みの合計は,
を加えたことによる伸び縮みの合計は,