


: 静止流体の圧力
: 連続体の力学
: 弾性率
長さ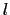 ,断面積
,断面積 の一様な棒に力
の一様な棒に力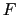 を加えて引っ張り,
を加えて引っ張り,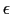 の伸び歪みを与えるためには,棒のヤング率を
の伸び歪みを与えるためには,棒のヤング率を とすると,
とすると,
となる.さらに,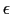 を
を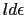 だけ増すためには,この力で棒の長さを
だけ増すためには,この力で棒の長さを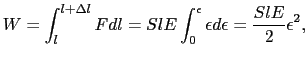 =
= 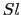 だけ増すわけであるから,
だけ増すわけであるから,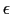 =
= 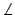 まで引っ張るときになされる仕事
まで引っ張るときになされる仕事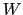 は,
は,
となる.棒の体積は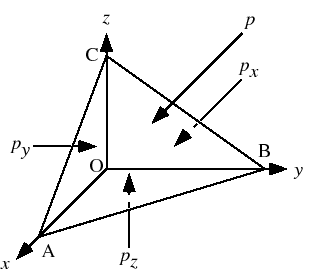 であるから,この棒には単位体積当り,
であるから,この棒には単位体積当り,
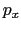 |
|
|
(6.3.9) |
だけの仕事が外力によってされたことになる.弾性体の場合,この仕事は内部にポテンシャルエネルギーとして蓄えられる.これを弾性歪みエネルギーという.
Masashige Onoda
平成18年4月15日
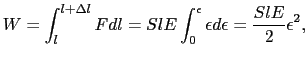 =
= 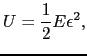
 であるから,この棒には単位体積当り,
であるから,この棒には単位体積当り,