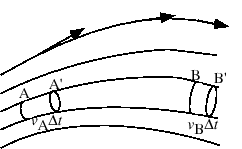
: 完全流体の運動
: 連続体の力学
: 弾性歪みエネルギー
液体と気体を総称して流体と呼ぶ.静止している流体の中に任意に一つの面を考えると,この面を通して異なった部分が互いに力を及ぼしあう.ただし,その応力は法線応力(圧力)だけで,接線応力は現れない.もし接線応力があると,流体は面に沿って自由に動くから,静止流体という仮定と矛盾してしまう.
図6.6のように,流体内の1点Oを頂点とし, ,
, ,
, 軸に平行な稜をもつ微小な四面体OABCを考えよう.
軸に平行な稜をもつ微小な四面体OABCを考えよう.
図 6.6:
 ,
, ,
, 軸に平行な稜をもつ微小な四面体OABC
軸に平行な稜をもつ微小な四面体OABC
|
|
各面に垂直にはたらく圧力を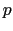 ,
,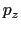 ,
,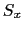 ,
,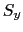 とし,
とし,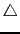 ABCの外向き法線の方向余弦を
ABCの外向き法線の方向余弦を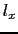 ,
,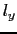 ,
,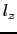 とする.
とする. 軸を鉛直上向きにとり,
軸を鉛直上向きにとり,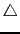 ABC,
ABC,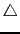 OBC,
OBC,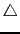 OCA,
OCA, OABの面積をそれぞれ
OABの面積をそれぞれ ,
,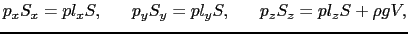 ,
,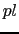 ,
,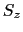 で表すと,各座標軸の方向に関して四面体の釣り合いを考えれば,
で表すと,各座標軸の方向に関して四面体の釣り合いを考えれば,
の関係が成立しなければならない.ここで は流体の密度,
は流体の密度, は四面体の体積である.(
は四面体の体積である.(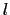
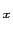 ,
,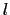
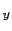 ,
,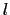
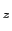 )を一定に保ったまま,面ABCを限りなくOに近づけていくと,
)を一定に保ったまま,面ABCを限りなくOに近づけていくと, や
や
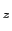 は稜の長さの二乗に比例して小さくなっていくが,
は稜の長さの二乗に比例して小さくなっていくが, は三乗に比例するので,上の第3式の重力の項は消え,
は三乗に比例するので,上の第3式の重力の項は消え,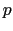
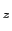

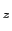 =
= 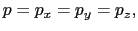
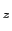
 としてよい.前にも述べたように,この四面体では,
としてよい.前にも述べたように,この四面体では,
という関係があるから,
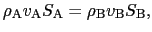 |
|
|
(6.4.10) |
が成り立つ.すなわち,圧力の大きさは面の方向によらない.このような圧力を静水圧という.圧力のSI単位をPa(パスカル)といい,
1 [Pa] = 1 [N/m
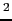
],
流体内の圧力は深さとともに増加する.その結果,流体内にある物体が表面から受ける圧力の合力は鉛直上向きとなる.この合力を浮力という.流体中の物体は,その物体がおしのけた流体の重さに等しい大きさの浮力を受ける.これをアルキメデスの原理という.
Masashige Onoda
平成18年4月15日
![]() ,
,![]() ,
,![]() 軸に平行な稜をもつ微小な四面体OABCを考えよう.
軸に平行な稜をもつ微小な四面体OABCを考えよう.