


: 粘性と抵抗
: 連続体の力学
: 静止流体の圧力
流体が運動しているときは流体の速度 が重要になる.
が重要になる. は,位置(
は,位置( ,
, ,
, )と時間
)と時間 の関数である.流れのいたるところで
の関数である.流れのいたるところで が
が によらない流れは定常流と呼ばれる.
によらない流れは定常流と呼ばれる.
各点の を表す矢印をたくさん描くと,矢印は連なって一群の曲線ができる.これらの曲線の接線がそこの
を表す矢印をたくさん描くと,矢印は連なって一群の曲線ができる.これらの曲線の接線がそこの と一致する.このような曲線を流線という.
と一致する.このような曲線を流線という.
流体が運動しているときには接線応力が現れる.粘っこい流体ほど大きな接線応力が生じるので,この性質を粘性という.ここでは粘性の無視できる理想的な流体,すなわち,完全流体を扱う.完全流体は運動していても,静止流体と同様に,面に垂直な圧力しかはたらかない.
図6.7のように,定常流の中に多数の流線によって囲まれた管(流管)を考えよう.
定常流であるから流管は動かず,一つの流管内の流体は管内を動くだけで管外に出ることはない.断面Aにおける流体の密度,速さ,断面積を,それぞれ
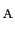 ,
,
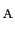 ,
,
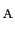 ,断面Bにおけるそれらを
,断面Bにおけるそれらを
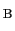 ,
,
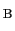 ,
,
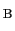 とおく.
とおく.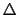
 時間後に断面Aにあった流体が断面A
時間後に断面Aにあった流体が断面A に,断面Bにあった流体が断面B
に,断面Bにあった流体が断面B に移動したとする.
に移動したとする.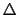
 の間にAとBの断面で区切られた部分では,
の間にAとBの断面で区切られた部分では,
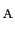

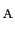

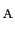
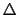
 だけの質量の流体が入り込み,
だけの質量の流体が入り込み,
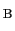

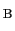

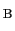
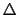
 だけの質量の流体が出ていったことになる.この部分の質量は定常流なら一定でなければならないので,流入量と流出量は等しいはずであるから,
だけの質量の流体が出ていったことになる.この部分の質量は定常流なら一定でなければならないので,流入量と流出量は等しいはずであるから,
となる.AとBは流管内の任意の断面であるから,
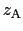 |
|
|
(6.5.11) |
という関係が成り立つ.これを連続の方程式といい,流体における質量の保存を表している.縮まない流体なら密度 は一定であるから,
は一定であるから,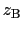 = 一定となる.
= 一定となる.
縮まない完全流体による定常流について,エネルギーの関係を考える.図6.8のように,一つの細い流管に沿って任意の2点A,Bをとり,それらの高さを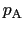 と
と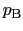 ,圧力を
,圧力を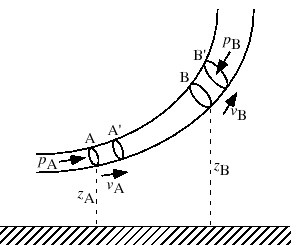 ,
,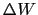 とおく.
とおく.
図 6.8:
縮まない完全流体による定常流に関するエネルギーの関係
|
|
AB間にある流体が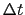 だけ時間がたって,A
だけ時間がたって,A B
B 間に移動するとすると,その間に流体に対してなされる仕事
間に移動するとすると,その間に流体に対してなされる仕事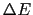 は,
は,
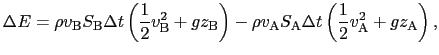 |
|
|
(6.5.12) |
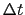 の間にAB間に含まれる流体の力学的エネルギーはA
の間にAB間に含まれる流体の力学的エネルギーはA B
B 間に含まれる流体の力学的エネルギーへ増加し,増加分
間に含まれる流体の力学的エネルギーへ増加し,増加分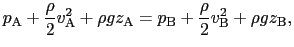 は
は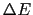 に等しくなければならない.定常流であるから,重複しているA
に等しくなければならない.定常流であるから,重複しているA B間の部分で何も変化せず,
B間の部分で何も変化せず,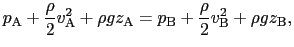 はBB
はBB 間とAA
間とAA 間に含まれる流体の力学的エネルギーの差ということになる.
間に含まれる流体の力学的エネルギーの差ということになる.
において
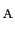

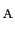 =
= 
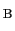

 を考慮すると,
を考慮すると,
が成り立つ.すなわち,1本の流線に沿って次の関係が得られる.
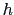 |
|
|
(6.5.13) |
これはベルヌーイの定理として知られている.
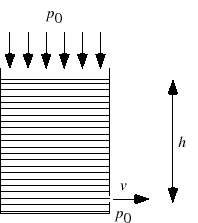
図6.9のように,容器内の液体が下の小さな孔から流れ出す場合を考えよう.
図 6.9:
容器内の液体が下の小さな孔から流れ出す場合
|
|
短い時間内では液面の高さは変わらずそこの流速は0で定常流と見なせる.孔と液面の距離を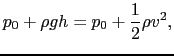 ,液体の流出する速さを
,液体の流出する速さを とすると,液面でも孔の位置でも圧力は大気圧
とすると,液面でも孔の位置でも圧力は大気圧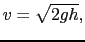 に等しいので,ベルヌーイの定理により,
に等しいので,ベルヌーイの定理により,
が成り立つ.これから,
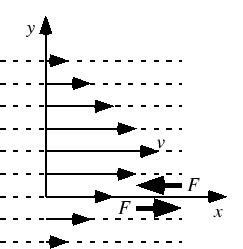 |
|
|
(6.5.14) |
が得られる.この関係をトリチェリの定理という.孔から流れ出す液体の速さは,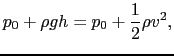 の高さだけ自由落下したときの質点の速さに等しい.
の高さだけ自由落下したときの質点の速さに等しい.
飛行機の翼の断面を図6.10に示す.上面が下面に比べて少し膨らんでいる.上面に沿って流れる気流は翼を避けるために狭い道を通るので,速さは下面のそれに比べて大きくなる.このために下面の圧力は上面に比べて大きくなる.これが揚力を得る主な原因の一つとなっている.



: 粘性と抵抗
: 連続体の力学
: 静止流体の圧力
Masashige Onoda
平成18年4月15日
![]() を表す矢印をたくさん描くと,矢印は連なって一群の曲線ができる.これらの曲線の接線がそこの
を表す矢印をたくさん描くと,矢印は連なって一群の曲線ができる.これらの曲線の接線がそこの![]() と一致する.このような曲線を流線という.
と一致する.このような曲線を流線という.
![]() と
と![]() ,圧力を
,圧力を ,
,![]() とおく.
とおく.
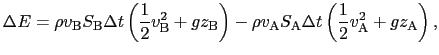
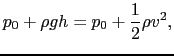 ,液体の流出する速さを
,液体の流出する速さを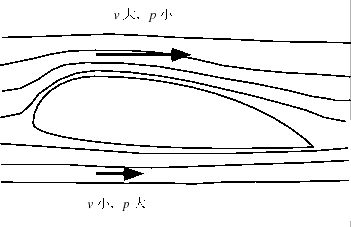

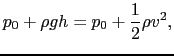 の高さだけ自由落下したときの質点の速さに等しい.
の高さだけ自由落下したときの質点の速さに等しい.