


: 第12回演習問題
: 連続体の力学
: 完全流体の運動
図6.11のように,ある点の近傍で 方向に平行に流れていて,速さ
方向に平行に流れていて,速さ が
が の関数で変化するものとしよう.
の関数で変化するものとしよう.
図 6.11:
ある点の近傍で 方向に平行に流れていて,速さ
方向に平行に流れていて,速さ が
が の関数で変化する場合
の関数で変化する場合
|
|
流体が完全流体でない限り,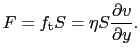 面に平行な面の両側で接線応力
面に平行な面の両側で接線応力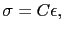 がはたらき,速い部分を遅く,遅い部分を速くしようとする.すなわち,
がはたらき,速い部分を遅く,遅い部分を速くしようとする.すなわち, 方向の速度勾配
方向の速度勾配
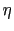 を減らそうとする.このとき
を減らそうとする.このとき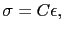 は
は
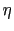 に比例するので,両面にはたらく力
に比例するので,両面にはたらく力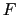 は,考える面の面積を
は,考える面の面積を とすると,
とすると,
 |
|
|
(6.6.15) |
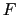 を粘性力,比例定数
を粘性力,比例定数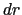 を粘性率という.
を粘性率という.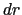 の単位は,
の単位は,
1 [N s m
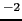
] = 1 [Pa s],
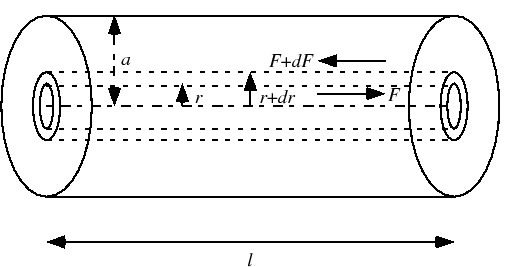
粘性率を測定する最も基本的な方法の一つを紹介しよう.図6.12のように水平においた長さ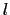 ,半径
,半径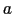 の一様な円管に目的とする液体を流し,左端に右端よりも
の一様な円管に目的とする液体を流し,左端に右端よりも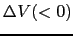 だけ大きい圧力がかかるようにして定常流をつくる.
だけ大きい圧力がかかるようにして定常流をつくる.
粘性流体では管壁のところは付着のために流速 は0になり,中心に近づくほど大きい.中心軸からの距離を
は0になり,中心に近づくほど大きい.中心軸からの距離を とおくと,
とおくと, は
は だけの関数
だけの関数 (
( )として与えられる.半径
)として与えられる.半径 と
と +
+ 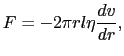 の面で限られ,長さ
の面で限られ,長さ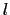 の薄い円筒部分の流体には,内側の円筒面を通じて
の薄い円筒部分の流体には,内側の円筒面を通じて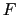 という粘性力が流れの向きにはたらく.同時に,外側の円筒面を通じて
という粘性力が流れの向きにはたらく.同時に,外側の円筒面を通じて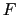 +
+ 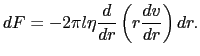 という力が流れの向きと逆向きにはたらく.(6.6.1)式より,
という力が流れの向きと逆向きにはたらく.(6.6.1)式より,
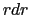 |
|
|
(6.6.16) |
となるので,
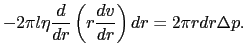 |
|
|
(6.6.17) |
この力がはたらいていても流体が定常的に流れるのは,両端に圧力差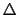
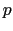 があるためである.円筒の切口部の面積が2
があるためである.円筒の切口部の面積が2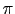
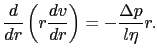 であるから,2
であるから,2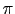
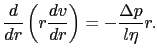
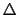
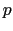 の力が流れの向きにかかっている.この力と
の力が流れの向きにかかっている.この力と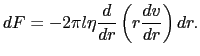 が釣り合っているのであるから,
が釣り合っているのであるから,
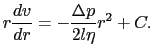 |
|
|
(6.6.18) |
すなわち,
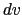 |
|
|
(6.6.19) |
積分すれば,
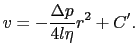 |
|
|
(6.6.20) |
定数 は,
は, = 0で
= 0で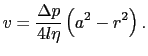 /
/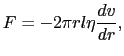 = 0であることから
= 0であることから = 0.さらに積分を行うと,
= 0.さらに積分を行うと,
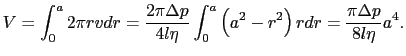 |
|
|
(6.6.21) |
 =
= 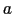 で
で = 0であることから定数
= 0であることから定数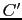 が決められる.
が決められる.
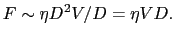 |
|
|
(6.6.22) |
単位時間にこの管の任意の断面を流れる流体の体積 は,
は,
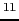 |
|
|
(6.6.23) |
すなわち,管右端から単位時間に流れ出る液体の体積を測ると,粘性率を決めることができる.この関係をハーゲン-ポアズイユの法則と呼ぶ.
流体が,静止している物体に向かって一様に速度 で流れるとき,物体には抵抗と呼ばれる力が流体から
で流れるとき,物体には抵抗と呼ばれる力が流体から の向きに作用する.この抵抗の原因は粘性にある.
の向きに作用する.この抵抗の原因は粘性にある.
いま,速度 の小さい流れの中で,静止している直径
の小さい流れの中で,静止している直径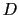 の球を考えよう.現実の流体では,物体表面に接した流体の粒子はくっついてしまい,表面上をすべることができない.そのために,球の近くでは流れが非常に減速される.そして接線応力の生じる領域は表面からかなり遠方にまでおよぶ.そのような領域内に存在する流体が粘性力によって減速される結果,反作用として球は
の球を考えよう.現実の流体では,物体表面に接した流体の粒子はくっついてしまい,表面上をすべることができない.そのために,球の近くでは流れが非常に減速される.そして接線応力の生じる領域は表面からかなり遠方にまでおよぶ.そのような領域内に存在する流体が粘性力によって減速される結果,反作用として球は の向きに力
の向きに力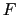 を受ける.これを粘性抵抗という.
を受ける.これを粘性抵抗という.
流速は球の表面から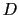 に等しい距離の範囲にわたり0から
に等しい距離の範囲にわたり0から まで直線的に変化すると考えると,速度勾配は
まで直線的に変化すると考えると,速度勾配は /
/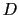 ,
,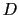
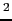 程度の面積にわたる接線応力は,
程度の面積にわたる接線応力は,
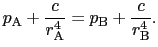 |
|
|
(6.6.24) |
 が大きくなってくると,表面に付着した流体の粒子はやはり動けないので,物体の表面近くに境界層と呼ばれる速度勾配の大きい部分ができ,境界層の外側では速度勾配がゆるやかな状態になる.さらに
が大きくなってくると,表面に付着した流体の粒子はやはり動けないので,物体の表面近くに境界層と呼ばれる速度勾配の大きい部分ができ,境界層の外側では速度勾配がゆるやかな状態になる.さらに が増すと,境界層は表面からはがれて,流体の後側には渦ができるようになる.この渦の部分では圧力が小さく,これに対して,物体の前面では流れが阻止される結果として圧力が高いため,物体は大きい力を受ける.これを慣性抵抗という.
が増すと,境界層は表面からはがれて,流体の後側には渦ができるようになる.この渦の部分では圧力が小さく,これに対して,物体の前面では流れが阻止される結果として圧力が高いため,物体は大きい力を受ける.これを慣性抵抗という.



: 第12回演習問題
: 連続体の力学
: 完全流体の運動
Masashige Onoda
平成18年4月15日
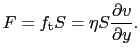 面に平行な面の両側で接線応力
面に平行な面の両側で接線応力
![]() ,半径
,半径![]() の一様な円管に目的とする液体を流し,左端に右端よりも
の一様な円管に目的とする液体を流し,左端に右端よりも![]() だけ大きい圧力がかかるようにして定常流をつくる.
だけ大きい圧力がかかるようにして定常流をつくる.
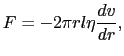 の面で限られ,長さ
の面で限られ,長さ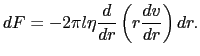 という力が流れの向きと逆向きにはたらく.(6.6.1)式より,
という力が流れの向きと逆向きにはたらく.(6.6.1)式より,
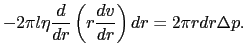
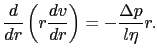 であるから,2
であるから,2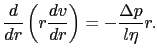
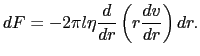 が釣り合っているのであるから,
が釣り合っているのであるから,
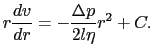
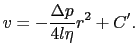
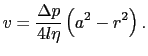 /
/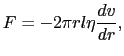 = 0であることから
= 0であることから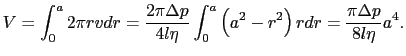
![]() で流れるとき,物体には抵抗と呼ばれる力が流体から
で流れるとき,物体には抵抗と呼ばれる力が流体から![]() の向きに作用する.この抵抗の原因は粘性にある.
の向きに作用する.この抵抗の原因は粘性にある.
![]() の小さい流れの中で,静止している直径
の小さい流れの中で,静止している直径![]() の球を考えよう.現実の流体では,物体表面に接した流体の粒子はくっついてしまい,表面上をすべることができない.そのために,球の近くでは流れが非常に減速される.そして接線応力の生じる領域は表面からかなり遠方にまでおよぶ.そのような領域内に存在する流体が粘性力によって減速される結果,反作用として球は
の球を考えよう.現実の流体では,物体表面に接した流体の粒子はくっついてしまい,表面上をすべることができない.そのために,球の近くでは流れが非常に減速される.そして接線応力の生じる領域は表面からかなり遠方にまでおよぶ.そのような領域内に存在する流体が粘性力によって減速される結果,反作用として球は![]() の向きに力
の向きに力![]() を受ける.これを粘性抵抗という.
を受ける.これを粘性抵抗という.
![]() に等しい距離の範囲にわたり0から
に等しい距離の範囲にわたり0から![]() まで直線的に変化すると考えると,速度勾配は
まで直線的に変化すると考えると,速度勾配は![]() /
/![]() ,
,![]()
![]() 程度の面積にわたる接線応力は,
程度の面積にわたる接線応力は,
![]() が大きくなってくると,表面に付着した流体の粒子はやはり動けないので,物体の表面近くに境界層と呼ばれる速度勾配の大きい部分ができ,境界層の外側では速度勾配がゆるやかな状態になる.さらに
が大きくなってくると,表面に付着した流体の粒子はやはり動けないので,物体の表面近くに境界層と呼ばれる速度勾配の大きい部分ができ,境界層の外側では速度勾配がゆるやかな状態になる.さらに![]() が増すと,境界層は表面からはがれて,流体の後側には渦ができるようになる.この渦の部分では圧力が小さく,これに対して,物体の前面では流れが阻止される結果として圧力が高いため,物体は大きい力を受ける.これを慣性抵抗という.
が増すと,境界層は表面からはがれて,流体の後側には渦ができるようになる.この渦の部分では圧力が小さく,これに対して,物体の前面では流れが阻止される結果として圧力が高いため,物体は大きい力を受ける.これを慣性抵抗という.