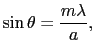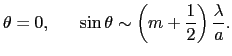: 第16回演習問題
: 波動
: 第15回演習問題
波は回折する.ここでは,フラウンホーファー回折を取り上げて,光の回折について考えよう.これは,光源も観測者も遮蔽から無限遠にある場合の回折7.1をさし,回折格子その他で実用上重要である.
幅が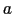 で,極めて細長いスリットに,波長
で,極めて細長いスリットに,波長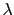 (
(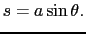
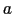 )の平行光が垂直に入射する.
)の平行光が垂直に入射する.
入射光の方向と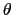 だけ傾いた方向に平行に進む回折光を考えよう.平行光ならば,無限遠でしか合致しないが,現実にはレンズを用い,その焦点に回折光を集めることにより,回折光の干渉を観察することができる.この場合,図7.16のA
だけ傾いた方向に平行に進む回折光を考えよう.平行光ならば,無限遠でしか合致しないが,現実にはレンズを用い,その焦点に回折光を集めることにより,回折光の干渉を観察することができる.この場合,図7.16のA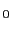 B
B からPまでの光学距離はどの回折光に関しても等しい.したがって,A
からPまでの光学距離はどの回折光に関しても等しい.したがって,A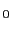 BとA
BとA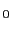 B
B で挟まれた部分における各回折光の光路差が問題になる.BB
で挟まれた部分における各回折光の光路差が問題になる.BB の長さ
の長さ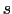 は,
は,
A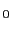 B間を
B間を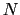 等分すると,各々の区分帯を通る回折光には
等分すると,各々の区分帯を通る回折光には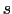 /
/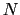 ずつの光路差がある.すなわち,A
ずつの光路差がある.すなわち,A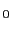 Bの位置では同位相でもA
Bの位置では同位相でもA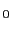 B
B の位置では順に,
の位置では順に,
の位相差が生じる.
光学距離の最も短い,A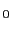 とA
とA の区間から出てPに達する光の振動
の区間から出てPに達する光の振動
 を,
を,
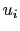 |
|
|
(7.5.76) |
とおく.ここで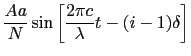 は幅
は幅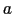 のスリットから傾き
のスリットから傾き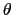 の方向に出る全回折光の振幅である.
の方向に出る全回折光の振幅である.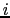 番目の区分帯から出る波のPにおける振動は,
番目の区分帯から出る波のPにおける振動は,
となる.すべての回折光のPにおける振動は,
で与えられる.積分表示にするために,
とおくと,
P点における明るさ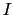 は,
は, の振幅の2乗に比例するから,
の振幅の2乗に比例するから,
![$\displaystyle I
\propto
\left [ {\sin (\pi s/\lambda) \over{(\pi s/\lambda)}} \right ] ^{2}.$](img1042.png) |
|
|
(7.5.79) |
これから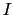 の極大・極小を求める.
の極大・極小を求める.
図 7.17:
回折光の明るさ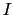 と傾き角
と傾き角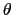 の関係
の関係
|
|
ここで,
とおけば,
より,
- 極小は
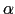 =
= 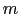
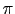 (
(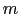 =
= 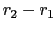 1,
1, 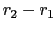 2,
2, 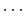 )のとき,すなわち,
)のとき,すなわち,
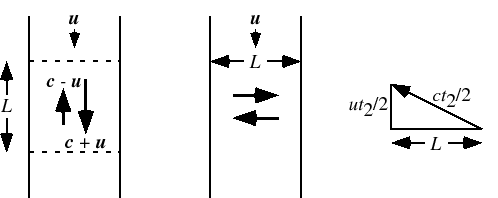 |
|
|
(7.5.80) |
で,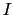 = 0.
= 0.
- 極大は
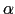 = 0または
= 0または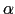 = tan
= tan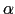 を満たす
を満たす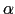 のとき,すなわち,
のとき,すなわち,
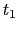 |
|
|
(7.5.81) |
回折光の明るさ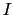 と傾き角
と傾き角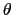 の関係を図7.17に示す.
の関係を図7.17に示す.



: 第16回演習問題
: 波動
: 第15回演習問題
Masashige Onoda
平成18年4月15日
![]() で,極めて細長いスリットに,波長
で,極めて細長いスリットに,波長![]() (
(![]()
![]() )の平行光が垂直に入射する.
)の平行光が垂直に入射する.
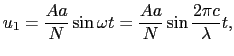
![]() とA
とA![]() の区間から出てPに達する光の振動
の区間から出てPに達する光の振動![]()
![]() を,
を,
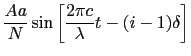 は幅
は幅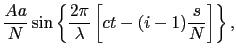
![$\displaystyle {Aa \over{N}} \sin \left [ {2\pi c \over{\lambda}}t - (i - 1)\delta \right ]$](img1035.png)
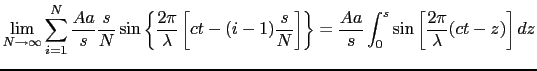
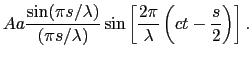
![$\displaystyle \lim_{N \to \infty} \sum_{i=1}^{N} {Aa \over{s}}{s \over{N}} \sin...
...a \over{s}} \int_{0}^{s} \sin \left [ {2\pi \over{\lambda}}(ct - z) \right ] dz$](img1040.png)
![$\displaystyle Aa {\sin (\pi s/\lambda) \over{(\pi s/\lambda)}} \sin \left [ {2\pi \over{\lambda}} \left ( ct - {s \over{2}} \right ) \right ].$](img1041.png)
![$\displaystyle I
\propto
\left [ {\sin (\pi s/\lambda) \over{(\pi s/\lambda)}} \right ] ^{2}.$](img1042.png)