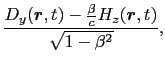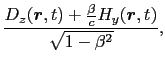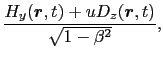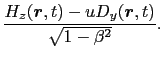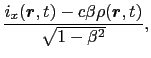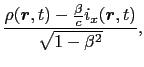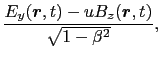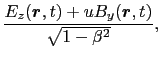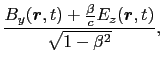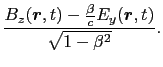: 第17回演習問題
: 特殊相対論への道
: 動く時計の遅れ
物体に対して静止している慣性系をO -
- 系(S
系(S 系)とし,それに対して
系)とし,それに対して 軸方向に
軸方向に の速度で運動している慣性系をO-
の速度で運動している慣性系をO- 系(S系)とする.このとき,両座標系における座標値の間には(8.2.19)式で表される関係がある.S系において,マクスウェルの方程式8.3,
系(S系)とする.このとき,両座標系における座標値の間には(8.2.19)式で表される関係がある.S系において,マクスウェルの方程式8.3,
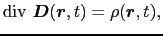 |
|
|
(8.6.28) |
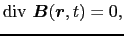 |
|
|
(8.6.29) |
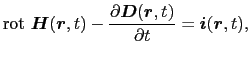 |
|
|
(8.6.30) |
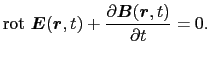 |
|
|
(8.6.31) |
が成り立っているとする.これらを物体に対して静止しているS 系に変換すると,どうなるだろうか?
系に変換すると,どうなるだろうか?
ローレンツ変換に伴って,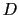 と
と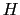 とが次のように変換されるとする.
とが次のように変換されるとする.
また,電流密度と電荷密度の変換は,
で与えられるものとする.さらに, と
と のローレンツ変換による変換性を次のように定める.
のローレンツ変換による変換性を次のように定める.
このとき,S 系においてもS系のそれとまったく同形のマクスウェルの方程式が成立する(証明略).
系においてもS系のそれとまったく同形のマクスウェルの方程式が成立する(証明略).



: 第17回演習問題
: 特殊相対論への道
: 動く時計の遅れ
Masashige Onoda
平成18年4月15日
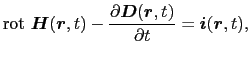
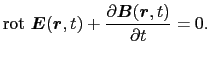
![]() と
と![]() とが次のように変換されるとする.
とが次のように変換されるとする.