半導体へテロ構造中の低電子密度領域の二次元電子系は、電子間相互作用に起因する多体効果の研究のための優れた対象です。半導体へテロ構造では、電子密度や電子-正孔間距離等のパラメターを外部から変えることができます。さらに電場、磁場を印加することにより、多体効果に起因する興味深い現象が数多く観測されています。低電子密度になるに従い、電子間相互作用に関わる現象が顕著になるのは、平均電子間距離をrsとすると、運動エネルギーはrs-2に比例するのに対して、電子間相互作用はrs-1に比例するため、rsが大きくなるに従い電子間相互作用が相対的に大きくなるからです。
低電子密度での二次元電子系の物性は興味深い現象の宝庫ですが、従来のドナーイオン層をもつ試料では不可避のドナーイオンによる散乱のため電子系が乱されていました。そこで、わたしたちはドナーイオン層をもたず、外部からの電場によって電子系を誘起する手法により低電子密度領域でも電子移動度の高い試料を用いて研究を行っています。
低電子密度領域の二次元電子系発光
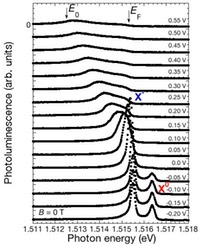
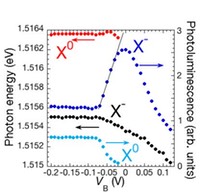
左上図に無磁場、温度T=100 mKにおけるゲート付き量子井戸試料の発光スペクトルのバイアス依存性を示します。裏面ゲートのバイアス電圧 が-0.05 Vより小さいところでは二つの発光ピークが見られます。1.5164 eVの高エネルギー側のピークが中性励起子( X0 )、低エネルギー側のピークが荷電励起子(X-)です。荷電励起子発光ピークの積分強度は電子密度に比例して増大します。電子密度が8x109 cm-2より低い領域では電子密度に比例して増大していることがわかります。それより高い電子密度では、比例関係からはずれ、二次元電子系+“自由な“正孔との間の光再結合による発光に移りかわります。電子密度を増大させると、発光の低エネルギー端のE0からフェルミ面EFまで拡がる二次元電子系の状態密度と電子占有を反映した発光に移り変わることがわかります。[固体物理、Vol. 44, No. 1 p. 43 (2009)]
低電子密度領域での有効質量の増大
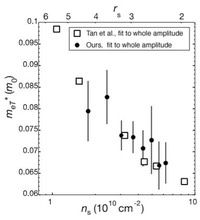
低電子密度領域で電子間相互作用が相対的に強くなると、電子はまわりの電子との相互作用によりその自己エネルギーが変化します。電子密度が下がるに従い、まわりの電子を”引きずる”ようにして電子の質量が増大します。この自己エネルギーを繰り込んだ準粒子有効質量は例えばシュブニコフ・ドハース(SdH)振動の振幅の温度依存性から見積もられるます。上図に私たちの測定結果とTan等の結果[Phys. Rev. Lett. 94, 016405 (2005)]を示します。電子密度の低下と共に電子の有効質量が増大していることがわかります。異なるグループの異なる試料構造で同様の結果を示していることから、測定で示された有効質量の増大が電子間相互作用によるものであり不規則構造によるものではないことを示しています。
[Phys. Rev. B 76, R201306 (2007)]
電子-正孔g因子の増大
二次元電子系に垂直方向に磁場を加えると、電子は上向きスピンと下向きスピンとで異なるエネルギーを持つようになります。このエネルギー差を磁場の大きさをB、ボーア磁子をμBを用いて
のように表されます。この中の係数g*effを有効g因子と呼びます。二次元電子系ではこの有効g因子が電子間相互作用により変化します。磁場中ではランダウ準位電子占有率νに応じて、上向きスピンと下向きスピンの電子数の差がν奇数において極大になります。そのため、ν奇数において上向きスピンと下向きスピンの電子のエネルギー差が極大となります。
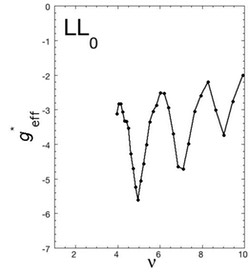
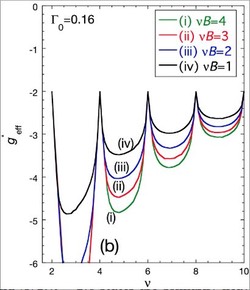
上図に発光スペクトルから測定された有効g因子のν依存性を示します。確かにν=5、7、9の奇数で有効g因子の大きさが極大となっていることがわかります。

上図に交換相互作用によるスピン分裂の増大と不純物散乱を取り入れた理論計算の結果を示します。この結果は測定結果を良く再現していることがわかります。このように電子間相互作用、今の場合、電子間交換相互作用によって発光スペクトルから測定された有効g因子の大きさの増大が説明されます。
[Phys. Rev. B 87, 085318 (2013).]
荷電励起子二次元電子-正孔のクロスオーバ
これまで、光学的手法による研究は非ドープ量子井戸試料を用いた研究が行われ、量子井戸中の電子密度が低い場合が調べられてきました。電子密度の低い場合には励起子または荷電励起子が観測されます。一方、電気的手法による研究ではドーパント層を持つ変調ドープされた試料を用いて、電子密度が高くて電流のよく流れる場合について調べられてきました。この場合、二次元電子系に満たされ、励起子と荷電励起子は観測されなくなります。この二つの極限の間の電子密度の薄い領域に物理として面白い現象が多く見られるのですが、両者のつながりは試料の問題であまり良くわかっていませんでした。私たちのゲート付き非ドープ量子井戸試料は、外部からの電場によって電子を0から高い密度まで誘起することができます。そこで、この試料を用いて二つの極限をスムーズにつなげて、両者の間で何が起こるかを調べました。
その結果、電子密度が増加するに伴って、二次元電子系によりクーロン相互作用が遮蔽される遮蔽長が減少することと、荷電励起子の半径が増大することとの間の対応関係を私達は、明らかにしました。遮蔽長が荷電励起子半径とほぼ一致する電子密度を境にして荷電励起子状態と二次元電子ガス正孔状態がクロスオーバーすることを見出しました。
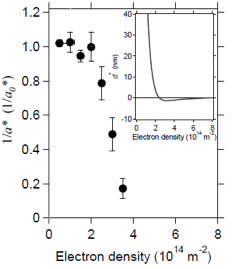
上図には荷電励起子半径の逆数(1/a*)の電子密度依存性を示します。電子密度が増すと急速にa*が大きくなることがわかります。電子密度が小さい領域では電子と正孔が強く結合した荷電励起子が形成されますが、電子密度が増大することにより、電子と正孔が乖離した二次元電子ガス正孔状態へとクロスオーバーすることがわかりました。
[Phys. Rev. B 87, 081310 (2013); Phys. Rev. Lett. 101, 207401 (2008).]
複合フェルミオン、分数荷電準励起子
強い磁場中の二次元電子系では、電荷が素電荷eの分数倍である分数電荷を持つ準粒子が観測されます。
強い磁場中では、一番低い準位(最低ランダウ準位)を全ての電子が占有し、全ての電子の運動エネルギーが同じになります。このため電子系の状態は電子間のクーロン相互作用のみで決まることになります。その結果、強磁場中の二次元電子系では、分数量子ホール効果等の興味深い現象が見られます。この系を直接的に考えるとクーロン相互作用の強い系ですので、解くのにむずかしい問題となります。そこで、J.K. Jainが考えたのが複合フェルミオン描像です。強い磁場中の電子を扱うにあたって、外部磁場(B)の一部を電子に付着させることを考えます。たとえば、上図のように各電子に2本ずつ磁束量子φ0を付着させるます。外部磁場は実効的に弱くなります(B*)。電子の描像では電子占有数がν=1/3だったものが、複合フェルミオンでは占有数ν*=1となります。その結果、電子の分数量子ホール効果は複合フェルミオンの整数量子ホール効果とみなすことができます。
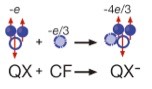
二次元電子系の励起状態は複合フェルミオンを用いると簡単に記述されます。さらに分数電荷をもつ複合フェルミオン(CF)と荷電励起子(QX)の束縛状態である分数荷電準励起子(QX-)が存在し得ることが導かれます。私達はν= 1/3近傍の発光スペクトルに、明確に分離された4-5つの発光ピークを初めて観測しました。その内の一つは準粒子励起(quasielectron)の存在するν≧1/3においてのみ観測されました。この観測結果は厳密対角化に基づく数値計算結果と比較され、分数荷電準励起子であることが示されました。
[Phys. Rev. B 89 (11), 115317 (2014).]